双方向型検査: 検査と構築の融合

可述的 System-F

System-F は元々、型の量化と特殊化の構文を入れた型付きラムダ計算だが、今回扱う言語では型推論を見据えて変数の型注釈を省略したり、明示的な特殊化ではなく型注釈から特殊化が自動的に行われるような体系を考える。具体的には、構文として以下のものを考える:

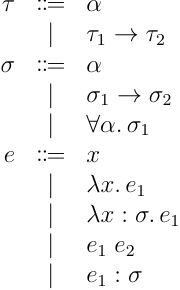
$\tau$ は単相型、$\sigma$ が通常の型、$e$ が項の構文となる。また、型システムの環境として、以下のものを使用する:

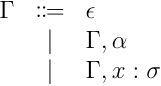
この時、以下の型システムを持つ言語が今回扱う対象になる:

前半3つが型の妥当性判定、後半が型付け判定になる。最後の2つが、型の量化と特殊化に当たる。通常、パラメータ多相を含む言語は、型変数の動く範囲について単相型のみを割り当てられるか、割り当てる型に制約が特にないか、つまり多相型ですら型変数によって割り当てられるかにより、言語全体の能力や性質が大きく変わってくることが知られている。前者を可述的 (predicative) であるといい、後者を非可述的 (impredicative) であるという。型推論においてもこの違いは大きく、一般に非可述的な言語の方が型推論が難しい。System-F は可述的な体系、非可述的な体系、それぞれ存在するが、今回は双方向型検査の紹介が目的なので、比較的難易度が低い可述的な System-F を対象として扱っていく。可述性は型システムにより決まり、今回の型付け判定では最後の型の特殊化規則で、置換が単相型に制限されている部分が可述性を決定づけている。これを、単相型でなく型全般にすると非可述的な体系になる。

Wells の結果 [1] から、このシステムにおいて型付け可能性、つまり以下の問題は決定不能であることが知られている:

項 $e$ について、$\vdash e: \sigma$ となる $\sigma$ は存在するか？

もちろん完全な型推論方法があれば、$\sigma$ の存在性は示せるため、逆に言えば完全な型推論も決定不能ということになる。

双方向型システム

これに対して、双方向型検査では、双方向の型システムを提供し、上記の型システムへの完全な型推論を諦める代わりに、双方向の型システムに対してはある程度完全な型推論アルゴリズムを提供する。双方向の型システムは以下のように定義される:

双方向型システムは2つの部分型関係 $\leq$、 $\preceq$ に依存するが、これについては後で見るとして、まずは双方向型システムの概要を見ていく。双方向型システムの判定は、

• $\Gamma \vdash e \Rightarrow \sigma$ は、$\Gamma$ の下で $e$ から型 $\sigma$ が構築される
• $\Gamma \vdash e \Leftarrow \sigma$ は、$\Gamma$ の下で $e$ は型 $\sigma$ で型付けできる

と読む。なお、紛らわしいので、元々の双方向でない型システムによる型付け判定を単方向型付け判定と呼ぶことにし、双方向型システムの判定をそれぞれ単に構築判定、型付け判定と呼ぶことにする。まず、単方向型付け判定と双方向型システムの対応関係を見てみる [2]:

このように、双方の部分型関係が反射的であり、$\leq$ が具体化を判定できるなら、ラムダ抽象、型の量化と特殊化に適宜型注釈をつけることで、元の型システムを尊重するような型構築ができる。この型注釈を適宜つけなければいけないというのが今回のポイントで、前述のように今回の対象言語は型注釈なしの項に対して決定可能な推論を提供できないため、今回の双方向型システムでは適宜型注釈を要求することで決定可能な範囲の推論にとどめるようになっている。これが完全な型推論を目指すアプローチと異なる部分になる。とは言っても、決定可能な範囲で推論を増強することは可能だ。例えば AbsSyn、AnnAbsSyn の規則は入れなくても単方向型付けとの対応は取れるが、これがない場合抽象に対して一々注釈を入れなくてはいけないようになってしまう。この後紹介する部分型関係の規則についても、決定可能な範囲で推論できる範囲を増やす為いくつか工夫が施されている。

さて、では部分型関係の方も見ていく。部分型関係はそれぞれ型の量化、具体化を自動でいい感じにやってくれるようなものになる。また、上記の話から反射性を満たし、$\leq$ については具体化をサポートする必要がある。また、単方向型付け規則に対する健全性への制約から、型注釈を足す程度で変換できる範囲での関係にしておく必要がある。この条件を満たすような $\leq$ 構成としては、例えば以下のようなものがある:

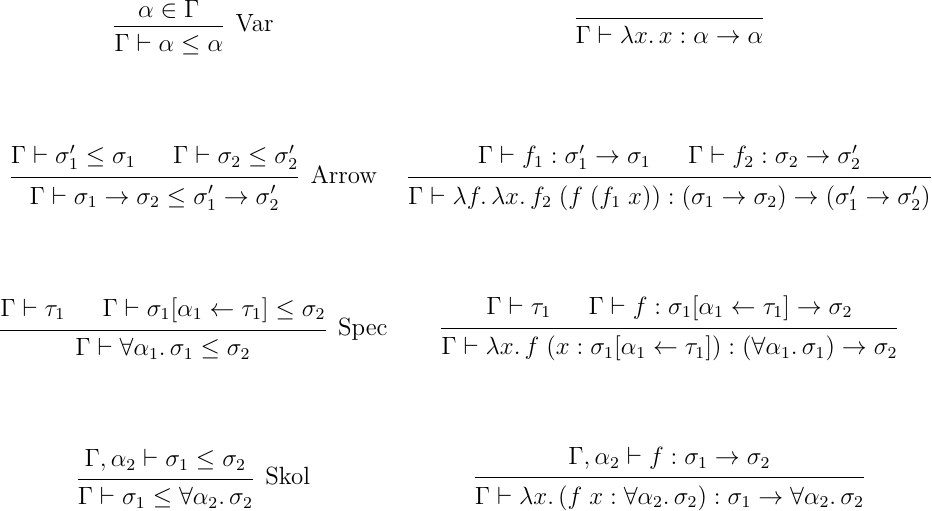
左が部分型関係の判定、右がその保証となる変換式になる。この定義であれば、変数、関数型はそのまま、多相型は Spec、Skol を組み合わせることで反射性を保証でき、特殊化もサポートしているため、条件を満たしている。さらに、この程度の判定であれば決定可能にできる。これについては後述する。$\preceq$ の方は、関数型への変換に特化した部分型関係となっており、適用の際暗黙的変換として使用される。こちらも、幾つかデザインの幅があると思うが、例えば以下のようなものがある:

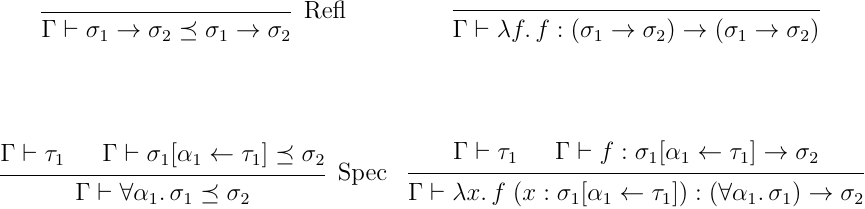
こちらは、基本的には型注釈をいい感じにつけて最終的に関数型に行きつくような範囲で、決定可能な判定が作れれば良い。例えば、以下のような判定を入れることもできる:

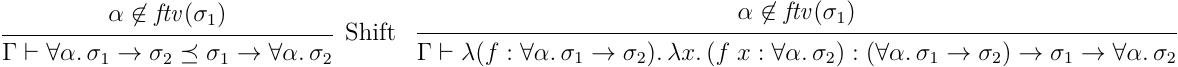
この拡張により、量化された型の構築ができる。まあ、今のところあまり有用な場面は思いついてないが、とりあえず関数型に行き着くような暗黙的変換の定義は色々できるという話。そこら辺は言語デザインに合わせて調整が必要になってくる部分だろう。ただ、暗黙的変換は一度採用してしまうとプログラマ側で変換を無効化すると言ったことができない。そこら辺は注意して設計するのが良いだろう。

さて、双方向型システムで型構築の導出をしてみた例が以下になる:

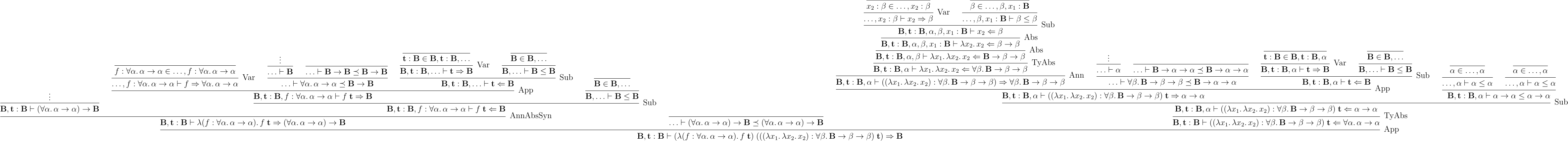
あまり型構築してるようには見えないかもしれないが、左から型を構築していき、構築した型を元に型付け判定をしていくのが基本的な流れだ。

推論アルゴリズム

さて、先ほどの導出例から分かる通り、双方向型システムはそれだけだと、アルゴリズミックに項に対して型を推論するのは難しい。ただし、この型システムに対して完全な、具体的に型を推論するアルゴリズムが構成可能だ。最後にこのアルゴリズムと、その構成の仕方を紹介しておく。

推論アルゴリズムの紹介に入る前に、まず型環境をアルゴリズム向けに拡張しておく:

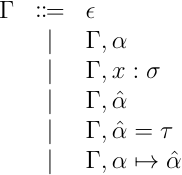
$\hat{\alpha}$ はアルゴリズム中で生成される変数を表す。$\hat{\alpha} = \tau$ は、$\hat{\alpha}$ が $\tau$ と等価であるという制約を表す。$\alpha \mapsto \hat{\alpha}$ は $\alpha$ が $\hat{\alpha}$ に置換されたことを表すマーカのような役割を持つ。詳細は、アルゴリズムを見ながら説明していく。もう一つ、アルゴリズムを説明する前に導入しておくものがある。それが型環境による置換だ:

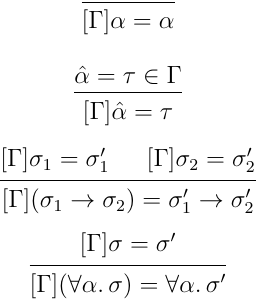
この置換では、環境内にある等価制約を使って、アルゴリズム中で生成された変数を置き換えていく。これをアルゴリズム中で適用していくことで、単一化の代わりにしているという感じだ。では、実際のアルゴリズムを見てみる:

相変わらず部分型関係の推論は後回しにすることにして、まずは判定の読み方だが

• $\Gamma \vdash e \Rightarrow \sigma \mid \Delta$ は、環境 $\Gamma$ が与えられた時、$e$ から $\Gamma$ を尊重するような環境 $\Delta$ と型 $\sigma$ が構築される
• $\Gamma \vdash e \Leftarrow \sigma \mid \Delta$ は、環境 $\Gamma$ が与えられた時、$e$ は $\Gamma$ を尊重するような環境 $\Delta$ の下で型 $\sigma$ に型付けできる

という感じ。まあ、大雑把には、$\Gamma$ に新しく生成した変数やら制約やらを入れた $\Delta$ が出力され、$\Rightarrow$ ではさらに型も出力される、$\Leftarrow$ は型 $\sigma$ が入力となっており、型検査が通るかがチェックされるという感じだ。この入出力を押さえておくと、双方向型システムから割と機械的に上記のアルゴリズム的型判定は生成できる。例えば、Abs 規則は、$\Gamma$、 $\lambda x\ldotp e$、 $\sigma_1 \to \sigma_2$ が入力として与えられるので、そこから $e$ に対してまた判定をかけて、出力の環境 $\Delta$ を得るという感じ。なお、このアルゴリズム的型判定では環境の順序が大事で、基本的に変数が生成されて環境に突っ込まれた場合その変数に関する制約はその位置に突っ込まれるようになっているため、基本最終結果に使用する変数以外の環境情報はいらない。なので、環境に生成された変数以外の何かを最後に突っ込んでおくと、それ以降に突っ込まれたものは最終結果には影響しないことが保証される。これについては、この後の部分型関係の推論と導出例で詳しくみる。もう一つ、AbsSyn の例を見ておくと、この場合は $\Gamma$、 $\lambda x\ldotp e$ だけが入力となっている。この場合、型も頑張って作らないといけない。ただ、これは正直よく分からん。というわけで、ブラックボックスのまま推論を進めるため、変数 $\hat{\alpha_1}$、 $\hat{\alpha_2}$ を当てがい、推論を進めてみて、その中で明らかになった制約を出力環境に保持したまま、生成した変数を使って出力の型を作るということをする。後は、出力に制約が含まれていたらそいつで置換、含まれていなかったら自由変数として放置すれば、いい感じの型になる。

さて、2つほどそもそも何が入出力かわからない部分があると思う。定義をまだ出していない部分型関係の推論を使っている、Sub規則、App規則だ。まず、Subの方だが、こいつは単一化兼一般化兼具体化みたいな役割担ってるやつで、環境 $\Gamma$、 型2つを入力として、その間に $\leq$ の関係が成り立つような、$\Gamma$ を尊重する環境 $\Delta$ を出力する。App規則の方は、$\Gamma \vdash \sigma_1 \preceq \sigma_2 \to \sigma_3 \mid \Delta$ のうち、$\Gamma$、 $\sigma_1$ が入力で、$\sigma_2$、 $\sigma_3$、 $\Delta$ が出力になる。こいつも、$\Gamma$ を尊重するような $\Delta$ と、$\Delta$ の下で $\preceq$ の関係が成り立つような $\sigma_2$、 $\sigma_3$ を計算するのが役割だ。

$\preceq$ の方が簡単なので、まずそちらから見てみる:

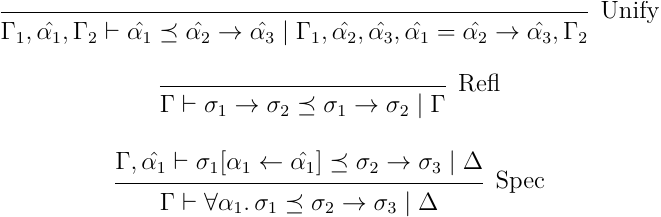
Refl は良い。Spec は元の規則通りだが、どういう具体化するか分からんので、そこを変数作ってブラックボックス化して凌ぐ感じ。で、元にない Unify というのが追加されているが、これが生成された変数にぶち当たった時用のやつで、この場合関数型になることだけ分かるので、関数型との等価制約だけ入れて、後の方はブラックボックスにして後続の推論におまかせという感じだ。ここで、制約を入れる位置が重要で、前述の通り元々の変数があった位置に入れることで、変数のスコープを調整している。

次に $\leq$ を見る。こちらはやや複雑:

前半が部分型の検査、後半がそれに伴う単一化という感じだ。前半はまあいいだろう。後半も実際はそれほど難しいことはしてなくて、単相型ならそのまま単一化、それ以外の場合は生成された変数か、関数型か、量化された型のいずれかなので、それぞれに規則があるという感じ。変数の場合は、環境の出現位置で順序をつけて、出現が早い方に単一化し、関数型の場合は両辺それぞれを単一化する。量化されてる型の場合だけ特殊で、この場合はどちらに量化された型が現れるかで Spec、Skol どちらの規則に合わせるかが変わるので、それぞれ調整している感じ。

こんな感じでやれば双方向型システムに対してある程度完全な推論がアルゴリズミックにできる。ある程度というのは、多少抽象度が高い推論をしてしまうことがあるかもしれないということで、残った変数に適宜型を割り当てられると完全になるみたいな感じ。さて、では実際に導出例を見てみる:

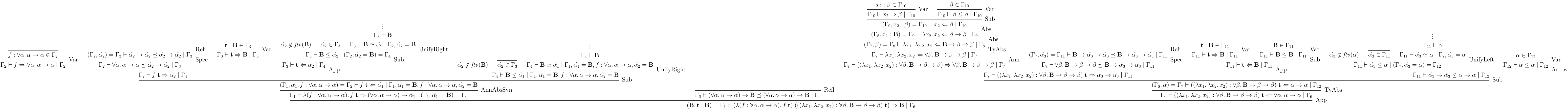
基本、推論に使う規則選びつつ、左から順にそのまま規則を適用していけば自然に導出が完成している。導出が完成しなければ推論失敗という感じ。あとは、規則を決定的にしてやれば、アルゴリズムになる。また、元の双方向型システムでの導出例と対応が取れてることも分かるだろう。このようにちゃんと規則が対応して適用できるようになっているため、完全な推論ができるという感じだ。完全性の証明は、題材には載ってないが Dunfield 先生が別途公開していて、https://research.cs.queensu.ca/home/jana/papers/bidir/ の Proofs から見れる。興味があれば見てみると良いだろう。

まとめ

というわけで、System-F の推論を考慮した双方向の型システムと、それに対する完全な推論アルゴリズムを紹介した。完全な推論はあれば便利だが、完全な推論ができない体系について言語の機能を落とさずにある程度実用的な推論を提供できるのは実用的には嬉しそうだ。ただ、双方向型システムは理論的にも面白いと思っていて、基本的に型推論の文脈では任意の項について主要型 (principal type) を見つける話から始まるわけだが、双方向型システムは主要型が決まる項と決めるのが難しい項を意味論として形式化できる能力があるところが面白いと思う。今回の System-F では、量化された型の導入は $\Leftarrow$ の判定しか持たない。逆に適用は $\Rightarrow$ しか持たない。これはそれぞれ、量化された型の導入について型付け判定はできるが主要型の探索は難しい、適用は部分項の型が決まれば主要型が自然に決まるみたいな性質に対応する。ここら辺は、一般的な (単方向の) 型付け判定より、言語の型のモデルをよく捉えられていると言えそうで、結構面白いなと思った。なお、じゃあ何かしら言語があった時、双方向の型システムをどうやって構成していけばいいかについては、

Jana Dunfield and Neel Krishnaswami. 2022. Bidirectional Typing. ACM Comput. Surv. 54, 5 (June 2022), 1–38. DOI: https://doi.org/10.1145/3450952

で、Dunfield 先生が step-by-step で解説してくれてる。これは割と参考になると思うので読んでみると良いんじゃないだろうか。

ところで、実はこの記事を書いたのは The appeal of bidirectional type-checking という記事がきっかけだった。この記事は「HM 推論はもう古い、これからは双方向型検査の時代！」という感じの文面 [3] で、まあそうなのかと乗せられた感じだ。ただ、導入部分で説明したように、そもそも HM 推論と双方向型検査ではかなりアプローチも達成できることも異なる。それに、HM 推論は具体的な体系に対する推論だが、双方向検査はより一般的な双方向の型システムに対しての検査を指す総称なので、比較対象としても成り立つかと言われると微妙だ。そして、双方向型システムをちゃんと一から構成するのはかなり難易度が高いと個人的には思う。なので、HM 推論周りの応用技術が使える範囲で済むなら、別に双方向型システムの方を採用する意義は薄そうだと思う。ただ、型システムをどんどん拡張していき、結構強い型の機能を入れていくなら、双方向型システムでモデル化してそこからアルゴリズムを作っていくのは結構合ってそうだ。別に難易度は易しくはないと思うが、無理に HM 推論を拡張するより扱いやすそうな印象がある (実用経験なしの言葉)。ま、一度触れてみて、HM 推論はもう古いとか言ってる人尻目に、自分の言語に合いそうだったら使っていくのがいいんじゃないだろうか。

ま、そんな感じで。今回はこれで。

[1]	(1, 2) J.B. Wells. 1999. Typability and type checking in System F are equivalent and undecidable. Annals of Pure and Applied Logic 98, 1–3 (June 1999), 111–156. DOI: https://doi.org/10.1016/S0168-0072(98)00047-5

[2]	これは Dunfield 先生の方の題材では完全性として提示されている関係性。題材には、証明は載っていないが、https://research.cs.queensu.ca/home/jana/papers/bidir/Dunfield13_proofs.pdf に証明が載っており、そこから復元したものになる。

[3]	まあ、そこまでは言ってないかもだが、ニュアンス的にはそんな感じの印象が強い。

[4]	元々 Scala や Agda を事例に出してたが、どちらも双方向型システムによるアルゴリズムは型検査に使ってなさそうだったので、訂正した。申し訳ない。