Let多相と型推論

単純型付ラムダ計算と型推論

Let多相の話に入る前に，まずは単純なものから話を始めていく．つまり，単純型付ラムダ計算の型推論を考えていく．単純型付ラムダ計算は，変数と定数，抽象，適用だけがある，単相な型の値しか作成できないような言語で，以下のような構文要素により構築される．

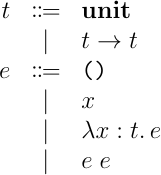
今回は定数として， unit 型の値 () のみを考えることにする．型システムは以下のように与えられる．

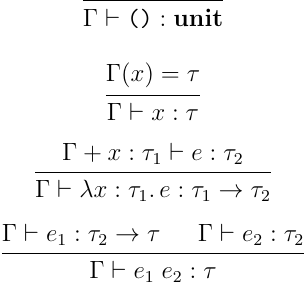
型安全性とかは今回はあまり興味はないので，評価モデルとかは省略する．さて，この体系に関しての型推論というのはいくつか考えられるが，今回考えたい問題は，式の構文要素から型指定を抜いたものに対して型チェックを満足させるような型を計算できるかというものだ．つまり，以下の型なしラムダ計算の式に対して型がつけられる場合はその型を，付けられない場合付けられない旨を出力するアルゴリズムが作れるかということになる．

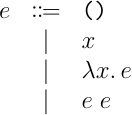
ちゃんと問題として形式化するなら，

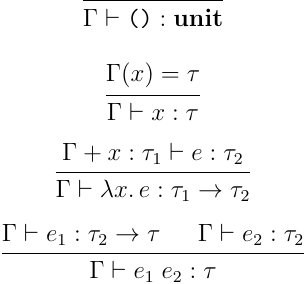
のような型システムについて，

型なしラムダ計算の項 $e$ に対して，$\vdash e: \tau$ を満たす $\tau$ が存在すればその $\tau$ を，存在しなければ $\bot$ を出力する

アルゴリズムを構築できるかというのが今回扱う問題になる．これを解くためのアルゴリズムは色々知られているが，今回は以下のようなアルゴリズムを考える:

この時，$\mathcal{W}_{\text{simply}}(\emptyset, e) = (S, \tau)$ の時 $\mathbf{default}(\tau)$，それ以外の時 $\bot$ を返すと問題の解になる．アルゴリズム中での $\mathcal{U}$ は単一化と呼ばれるアルゴリズムで，以下を返す:

$S\tau_1 = S\tau_2$ を満たす置換 $S$ がある時，$\mathcal{U}(\tau_1, \tau_2) = S$

アルゴリズム $\mathcal{W}_{\text{simply}}$ は基本抽象の変数の型を変数としておいておき，単一化により型チェックが通る範囲まで型を具体化する．例えば，$(\lambda f\ldotp \lambda x\ldotp \lambda y\ldotp f\; y)\; (\lambda x\ldotp x)\;\text{\texttt{()}}$ に対して，この推論アルゴリズムは次のように動く:

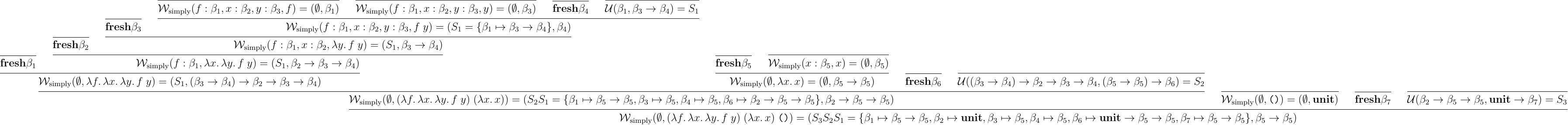
イメージとしては，以下のような感じ:

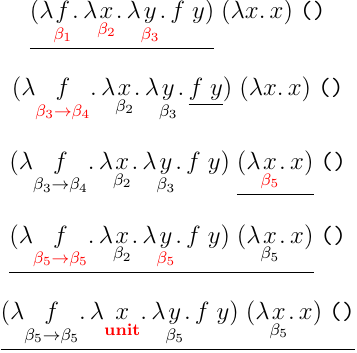
抽象の各変数に型変数を割り当てていき，各式を見て単一化により型を具体化していく．このようにして，単純型付ラムダ計算の型推論は行える．

Let多相

さて，先ほど見た単純型付きラムダ計算は単相的な型，つまりパラメータなどを持たない型としか扱えない．なので，例えば次のようなプログラムは型付けできない:

先ほど紹介した型推論アルゴリズムでこのプログラムの型を推論しようとすると，

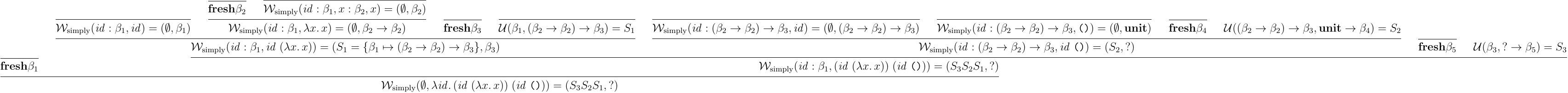
のように途中で $(\beta_2 \to \beta_2) \to \beta_3$ と $\mathbf{unit} \to \beta_4$ のような型を単一化しようとして失敗する．これは，変数 $\mathit{id}$ を関数に適用する箇所と，$\mathbf{unit}$ 型の値に適用する箇所の二つがあるためだ．$\mathit{id}$ を関数をとる関数型として扱うと後者が立たず，逆に $\mathbf{unit}$ 型の値をとる関数型として扱うと前者が立たない．これが単一化の失敗に現れており，この式に正当な型をつけることはできない．これを回避するには，

のようにそれぞれ必要な型ごとに変数を用意する必要がある．$\mathit{id}$ の実装としては $\lambda x\ldotp x$ が関数を受け取る場合も $\mathbf{unit}$ を受け取る場合も適合する．しかし，単純型付ラムダ計算の世界ではこの実装も型によってそれぞれ書く必要がある．しかし，これはモジュール性の観点からも再利用性の観点からも微妙だ．

そこで，多くのプログラミング言語は多相型を持つ値を作れるようにすることである程度この問題を解決している．具体的には，

のように書くと，$\mathit{id}$ は関数を受け取る部分では $\alpha$ を適合する関数型に，$\text{\texttt{()}}$ を受け取る部分では $\alpha = \mathbf{unit}$ にと，それぞれの使用箇所で適合する型をパラメータに入れて，それで型付できればよしとするようなシステムを搭載している．これにより，多相型を持つ値を作ってそれを公開するようにすれば，使用箇所でわざわざ実装を書き直すことなく型を変えて使用することができ，実装と使用箇所を分離して管理することができるようになる．

さて，表現力の観点からも多相型を入れた体系は理論的に幾つか提唱されており，特に単純型付ラムダ計算にパラメータ多相を入れた拡張として System F という体系がある．System F は多相型の値を単装型の値と同じように扱うことができ，かなり強力な拡張になる．ただ，System F は完全な型推論が不可能であることが知られている [2]．現実的には，プログラミング言語の機能として，System F ほどの強力な拡張はいらずある程度型推論ができる体系が欲しくなる場合が多い．そこで，多相型の値の作成方法と扱い方を単装型に比べて制限した上で，完全な型推論が行える体系として Let 多相というものが提唱されている．Let 多相は先ほどの単純型付ラムダ計算の構文に，let 構文と呼ばれるものを足す．構文の全体は以下のようになる:

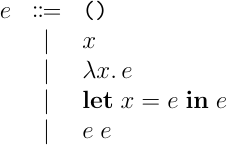
let 構文は，多相型を持つ値を作成できる構文で，この構文で束縛された変数のみ多相型を持って良いということになる．Let 多相では型は単相型と多相型の二種類を持ち，それぞれ以下のような構文を持つ:

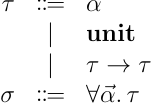
単相型 $\tau$ は基本単純型付ラムダ計算の時と変わらないが，変数 $\alpha$ が許容される点が異なる．ただし，変数を含んでいても式 $e_1$ では変数に関数型を，$e_2$ では変数に $\mathbf{unit}$ 型をというような使い分けはできず，変数には何か一つの型を固定して単相的に紐づけることしかできない．逆に，多相型 $\sigma$ は内部にパラメータを持ち，そのパラメータに応じて単相型を変えることができる．Let 多相の型付規則は以下のようになる:

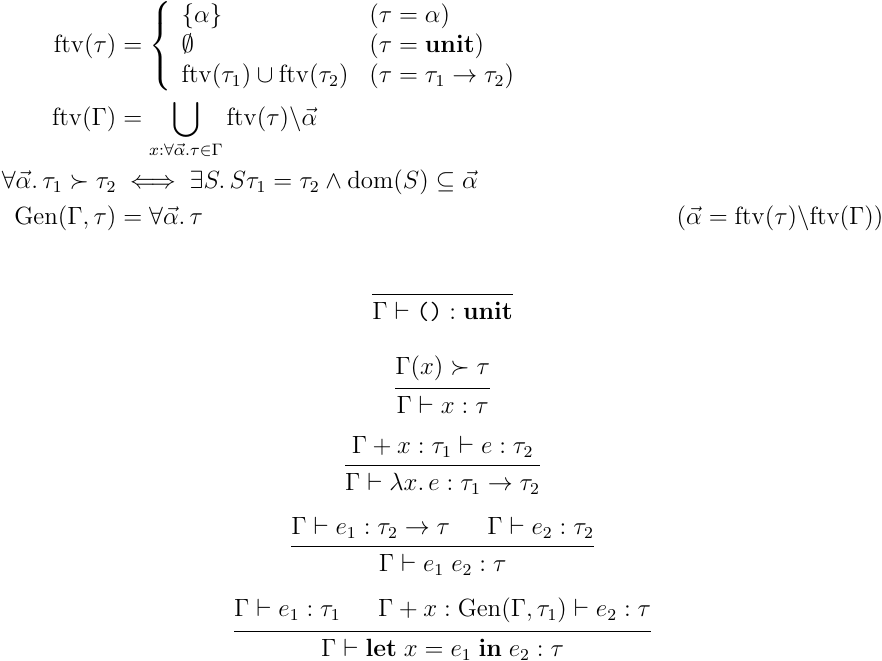
$\sigma \succ \tau$ はインスタンス化と呼ばれ，多相型 $\sigma$ のパラメータに何かしら単相型を紐づけたものが $\tau$ であると読む．$\mathrm{Gen}(\Gamma, \tau)$ は一般化と呼ばれ，単相型 $\tau$ に含まれる変数をパラメータ化して多相型を返す操作になる．Let 多相は，環境に多相型を持つ変数を含む．しかし，その変数が式中で使われる場合はインスタンス化して使わなければいけないというのが変数の規則になる．抽象と適用は単純型付ラムダ計算の際と同じで，抽象の際環境に入る変数は，パラメータのない多相型として追加される．let 構文では，変数に束縛する式の型を一般化して，型が具体化されていない部分はパラメータとして扱って良いということを示している．Let 多相の型推論とは，この型システムに対して，

Let 多相の項 $e$ に対して，$\vdash e: \tau$ を満たす $\tau$ が存在すればその $\tau$ を，存在しなければ $\bot$ を出力する

アルゴリズムを構築できるかという問題になる．

Let 多相の型推論

この型推論アルゴリズムは，単純型付ラムダ計算の時に紹介したアルゴリズムを let 構文に対して拡張することで得られる:

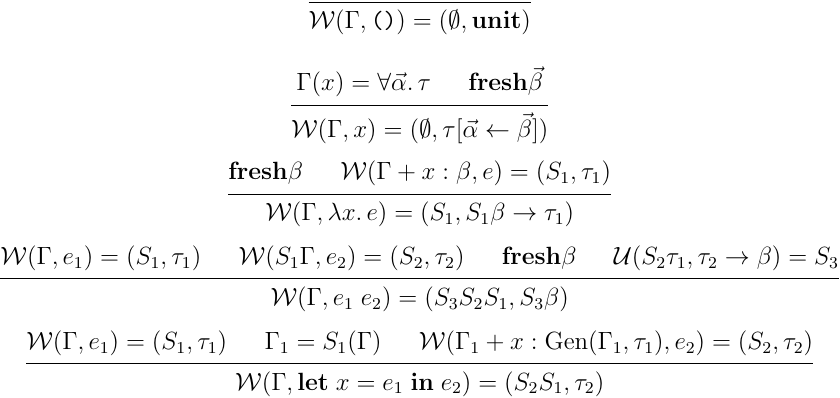
この時式 $e$ について，$\mathcal{W}(\emptyset, e) = (S, \tau)$ の時 $\mathbf{default}(\tau)$，それ以外の時 $\bot$ を返せば，型推論アルゴリズムとなる．単純型付ラムダ計算の時と異なるのは，インスタンス化と一般化の部分，すなわち変数の規則と let 構文の規則で，その他は基本単純型付きラムダ計算の時と同じである．考え方も基本同じで，ただ多相型から変数が参照される際にインスタンス化されること，let 構文では一般化が起きることが起きるようになることが付加されるという感じだ．

導出例は以下のようになる:

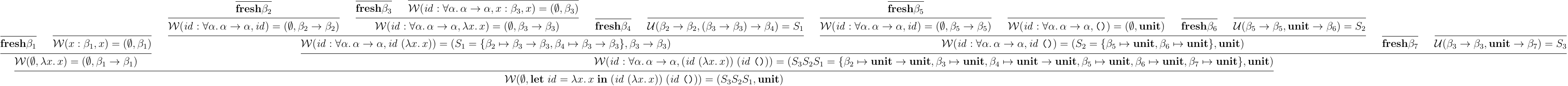
イメージとしてはこんな感じ:

変数 $\mathit{id}$ に行き着いたところどころで，インスタンス化によって新たに変数が置かれるのがポイントだ．これにより，同じ変数 $\mathit{id}$ でも出現位置が異なると異なる型を持てるようになる．

なお，Milner 先生の元文献では Algorithm J という Algorithm W の再代入可能な変数を使った効率良い版の実装も紹介されているので，興味がある人は見てみると実装の参考になるかもしれない．

さて，一応題材として扱ったやつにも触れておくと，今回の題材では Algorithm W とは別に Algorithm M という別の let 多相の推論アルゴリズムを考案している．Algorithm W は適宜型が分からない部分で変数を導入し推論を進め，部分式についての型の情報が揃った段階で単一化することで型の具体化と競合がないかのチェックを行なっていた．しかし，この方式は，型エラーが単一化まで先延ばしにされ，分かりにくいという問題がある．Algorithm M はその問題を解消するため，最後に一気に単一化を行うのではなく，ある程度できる単一化を早期に徐々に進めていこうといった感じの型推論アルゴリズムになる．具体的には以下のようになる:

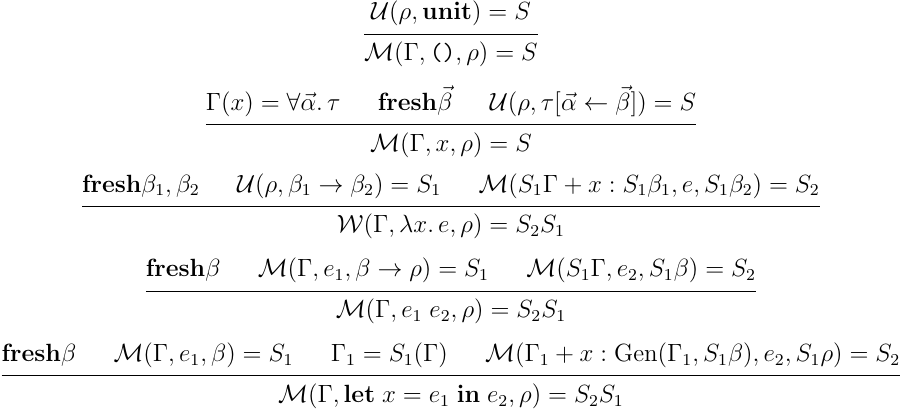
この時，式 $e$ について，$\mathcal{M}(\emptyset, e, \beta) = S$ の時 $\mathbf{default}(S\beta)$，それ以外の時 $\bot$ を返せば，型推論アルゴリズムとなる．基本的には，与えられた式の型を変数としておき，それを部分式について推論を進める途中節々で単一化をかけて，徐々に具体化していくという感じだ．導出例は以下のようになる:

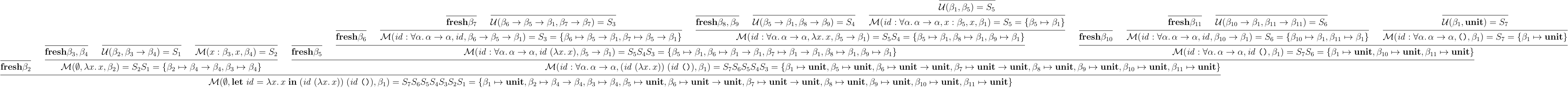
正直どっちがいいかは場合による気がするが，まあこういうアルゴリズムもあるよという感じだ．こんな感じで Let 多相であれば完全なアルゴリズムを与えられる．正当性とかに興味があれば，題材と Milner 先生の方のを見てみると良いだろう．

単一化の実装

さて，ここまで Let 多相の推論について扱ってきたが，推論アルゴリズムは基本単一化というアルゴリズムを基に構築されており，重要なパーツになっている．最後にこの単一化の部分について少し触れておこう．単一化は何も型の文脈だけで重要なアルゴリズムではなく，論理プログラミング，パターンマッチなどでも根幹をなす概念で，要は変数を含む項が2つあった時，その変数の部分いい感じに弄れば同じにできるかというのを解くアルゴリズムだ．ただ，体系によって結構決定不能になったり，効率があまり良くできないといった問題があるので注意が必要な問題でもある．

さて，今回扱う範囲の単一化は，俗に first-order unification と呼ばれる問題の範疇になる．要は単純な木で表現できる，変数とコンストラクタで構成される項の単一化は大体どういう構文を持っていても似たようなアルゴリズムが用意できるということだ．ついでに，higher-order，つまりラムダ項などを入れ正規化後の項が一致するかみたいな問題は決定不能になることが知られている．つまりは，型システムに型関数みたいなもの入れた状態で，Algorithm W のような型推論入れようとすると基本決定不能になる．なので，今回は first-order unification の範囲なので，アルゴリズムはいくつか知られたものがあるが，現実的には型システム強化しすぎると一筋縄でいかなくなるので注意が必要という感じ．

first-order unification のアルゴリズムはいくつか知られているが，中でも Martelli-Montanari Algorithm [3] が有名なものかな [4]．基本的には以下のようなアルゴリズム:

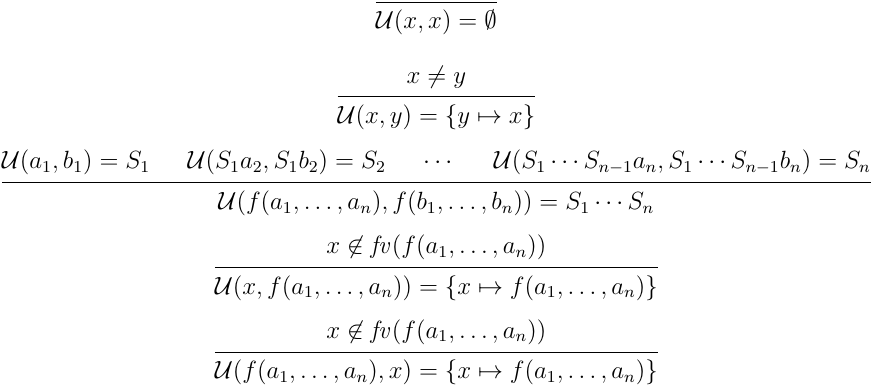
単純に項の根から一致しているか見ていって，変数部分は代入で両者一致するよう置き換えていきましょうというやつ．$\tau_1 \to \tau_2$ を2引数のコンストラクタ $(\to)(\tau_1, \tau_2)$，$\text{\texttt{()}}$ を0引数のコンストラクタだと思ってこのアルゴリズムを使うと，単一化ができる．

まとめ

というわけで，Let 多相とその推論アルゴリズムの紹介だった．あんまりネット上でこういうのまとめてる文献見つからなかったので，自分の参照用という側面が強いが，まあなんかお役に立てばという感じ．

型付ラムダ計算ベースの多相型を導入している言語は，それぞれが色々創意工夫をしてはいるものの，基本はこれらのアルゴリズムをベースにしていることが多い．なので，ここら辺理解しておくとエラーメッセージの気持ちを読み取りやすくなったりする [5]．興味があれば学んでみて損はないだろう．

今回はこんな感じで．

[1]	正当性とか諸々をすっ飛ばせば，Algorithm W，Algorithm J とかの部分は普通に理解できるだろうし．

[2]	J.B.Wells. Typability and typechecking in system f are equivalent and undecidable. Annals of Pure and Applied Logic, 98:111–156, 6 1999.

[3]	Alberto Martelli and Ugo Montanari. An efficient unification algorithm. ACM Transactions on Programming Languages and Systems, 4:258–282, 4 1982.

[4]	ここら辺はあんまり知らん領域なので良く分からん．SAT へのエンコード方法とかあったりするんかな?

[5]	正直アルゴリズム理解しないと読み取れない型エラーもどうかと思うが...