HM(X): 多相と制約と推論と

制約

今回扱う言語は基本的には Let 多相を搭載した型付ラムダ計算の拡張になる:

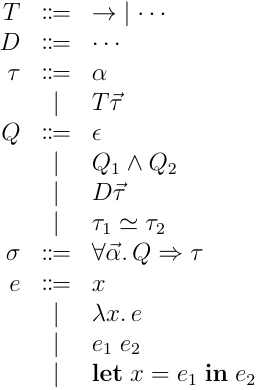
本来，HM(X) は制約に関して具体的な構文要素を用意せず，一定の性質を持ち推論解決アルゴリズムが存在するような抽象的な制約システムに対しての推論体系を提供する．ただ，今回はもう少し掘り下げて，具体例と制約解決アルゴリズムについても言及するため，あえて制約についても具体的な構文を用意している．各構文要素は以下のようになる:

型コンストラクタ $T$

型の等価判定の基本単位．原始的に関数型のコンストラクタ $\to$ を含んでいる．それぞれの言語によって導入される型コンストラクタは変わる．

制約コンストラクタ $D$

制約の等価判定の基本単位．それぞれの言語によって導入される制約コンストラクタは変わる．

型 $\tau$

型を表す項．変数と型コンストラクタから生成される．${\to}\; \tau_1\; \tau_2$ は $\tau_1 \to \tau_2$ と表記することもある．

制約 $Q$

制約を表す項．制約がないことを表す空制約 $\epsilon$，制約の結合，型制約，等価制約から生成される．

型スキーム $\sigma$

多相型を表す項．型パラメータ，パラメータを含んだ制約，パラメータを含んだ型から生成される．

式 $e$

式を表す項．変数，λ抽象，適用，let 式から生成される．

制約はそのまま言語機能として組み込んでもいいが，elaboration の対象として，他の言語機能を模倣するのにも応用できる．例えば，加算，乗算ができる型とそうでない型がある言語で，多相的な加算演算子，乗算演算子を提供したい場合を考える．具体的には次のようなコンストラクタを提供する言語を考える:

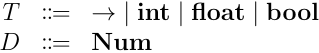
この場合に，

のようなプログラムにおいて， $\mathit{plus}$ は $\forall \alpha\ldotp \mathbf{Num}\; \alpha \Rightarrow \alpha \to \alpha \to \alpha$，即ち $\mathbf{Num}$ 制約を満たす型パラメータ $\alpha$ の引数を2つ受け取りその加算結果を計算して返すような多相関数として提供され，また $1.0$ は $\mathbf{float}$ 型の値として提供されたとき，それを元に $\mathit{double}$ は $\forall \alpha\ldotp \mathbf{Num}\; \alpha \Rightarrow \alpha \to \alpha$ として推論され，let 式の主部では $\mathit{double}$ の型パラメータ $\alpha$ が $\mathbf{float}$ 型にインスタンス化され，上記プログラム全体としては $\mathbf{float}$ 型の式と推論される，もし $\mathit{double}$ に $\mathbf{bool}$ 型の値を渡すと型推論が失敗する，というようにパラメータに関して何かしら条件を科すような機能を持った言語について，コンストラクタと提供する原始関数につける制約を工夫することで HM(X) の枠組みの推論体系を流用できるというわけだ．原著でも，サブタイプ関係を伴った推論や多相レコードを使った項への推論への応用例を挙げている．ま，動機としてはそんな感じ．

型推論

では，具体的に型システムと推論体系を見ていく．まず，型システムを見ていくが，その前に環境を用意しておく:

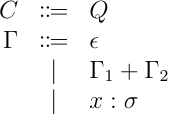
今回の制約付き Let 多相では，型付けを型環境 $\Gamma$ の他に制約環境 $C$ を元に判定する．型環境は言わずもがなだと思うが，制約環境とは今充足していることが保証される制約が入っている環境だ．今回は，制約と同じものしか入れないことにするが，例えば制約環境のみ特別な制約を導入することも可能だ．このような環境に対して，制約含意と型システムが定義される．

制約付き Let 多相の型システムは制約含意 $C \Vdash Q$ に依存する．制約含意とは制約環境から導かれる制約の判定のことで，以下のようになる:

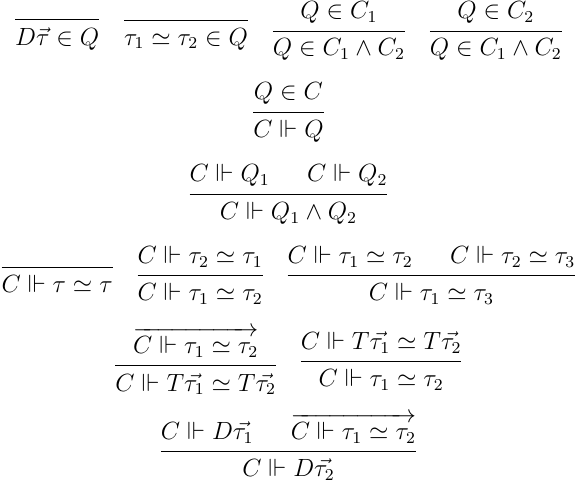
基本的な含意の規則は最初の2つで，後は型の等価判定制約に関する要求規則という感じだ．型の等価判定に対して特別な要求規則が入っているのは，おまけという意味合いも強いだろう．単純な構文的等価性の範疇を超えた型の等価性を扱う言語も多いし，等価性がパラメータの制約により影響を受ける言語も多い．その為，型の等価性，要はキャスティングについての拡張も考慮できるように型の等価判定を加えているという面が強くそこまで本質的な機能ではないと思われる．ま，これに関しては型判定の規則も見てみる方がいいと思うので，型判定の規則も示しておく:

前回 は Let 多相のイントロも兼ねてアルゴリズムに素直に対応する型システムを紹介したが，今回は一般化とインスタンス化を規則として分けて書いている．ただ比較がしにくいと思うので，HM(X) での加筆点を赤で示している．この赤の部分がなければ，普通の Let 多相の型規則ということになる．変数以外の式は一般化をしない限り多相型でない単相型の型でしか型付できず，部分項についても単相化されていることを要求している．let 式のみ束縛部分で使用する式に限り型スキームで型付されていることが許される．最後の2つの規則が一般化とインスタンス化に対応し，一般化では新たなパラメータと制約を導入することができ，インスタンス化ではパラメータ全てに単相な型を割り当てることと制約が満たされていることが要求される [1]．また，型の等価判定が成り立つ範囲ではキャストができるというのが，最後から3つ目の規則になる．

インスタンス化では制約含意を仮定においているが，これと制約含意の最後の規則により，型の等価判定の範囲であればインスタンス化する型を実際の型制約で使った型と同じにしなくても良くなる．ただ，導出としては制約含意での制約のキャストをするのでも，一度インスタンス化してからキャストの規則を使って型を変えるのでも問題ない．このキャストの規則と制約含意の規則の釣り合いが取れるようにというのと，無茶なキャストができないように制約含意の方にも型の等価制約に関する幾つかの要求規則が仕込まれているという感じだ．

さて，見ての通り HM(X) の型システムはそれほど大した拡張ではない．キャストの規則を追加して，制約込みで一般化できるようにし，インスタンス化の際制約のチェックが入るようになっただけだ．実際，推論の方もそこまで複雑な拡張を入れないで実現できる:

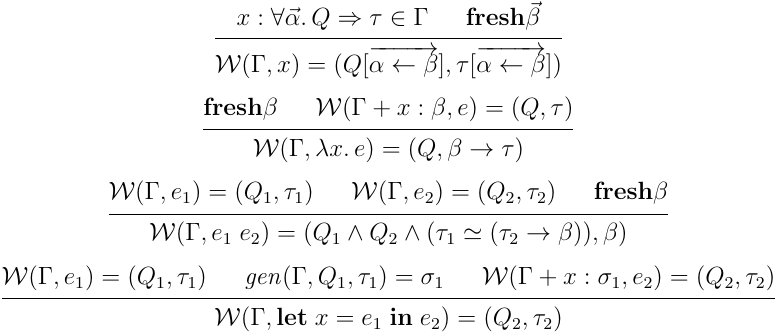
$\mathit{gen}$ は一般化関数で，$\mathit{gen}(\Gamma, Q, \tau)$ は $\vec{\alpha} = (\mathit{ftv}(Q) \cup \mathit{ftv}(\tau)) \backslash \mathit{ftv}(\Gamma)$ をパラメータとし，$\forall \vec{\alpha}\ldotp Q \Rightarrow \tau$ を返す [2]．

さて，この時，制約解決関数 $\mathit{solv}$，式 $e$，環境 $\Gamma$，制約環境 $C$ について，$\mathcal{W}(\Gamma, e) = (Q, \tau)$ で，$\mathit{solv}(C, Q) = S$ の時 $S\tau$，それ以外の時 $\bot$ を返せば，型推論アルゴリズムとなる．この時，制約解決をいい感じに設計すると，$C; \Gamma \vdash e: S\tau$ となるような推論が行えるアルゴリズムになる．今回は制約解決は具体的に後で構築し，あまり抽象的に「いい感じの設計」というのがどういう性質を指すかは立ち入らない．興味があれば元論文を読んでみるのがいいだろう．ま，基本的には制約解決の条件は $C \Vdash Q$ を満たし，$Q$ に含まれる型の等価性に関する制約が全て置換 $S$ に反映されていることという感じだ．こんな感じの設計を満たせば，大体制約込みの型推論になる．

一般化が制約込みで行われるようになること，単一化が型の等価性制約の追加，そして最後に制約解決が入ることのみが異なるが，基本アルゴリズム W と構成は同じだ．このように，HM(X) では与えられる制約システムにおいて，制約解決の方法が与えられた時，それを元に HM 推論を構成はほとんど変えずに拡張できる．

例えば，

について，$C = \mathbf{Num}\; \mathbf{float}$，$\Gamma = 1.0: \mathbf{float} + \mathit{plus}: \forall \alpha\ldotp \mathbf{Num}\; \alpha \Rightarrow \alpha \to \alpha \to \alpha$ の下での型推論を考えてみる．この時，まずは以下のように，$\mathcal{W}$ による制約と型の生成が行われる:

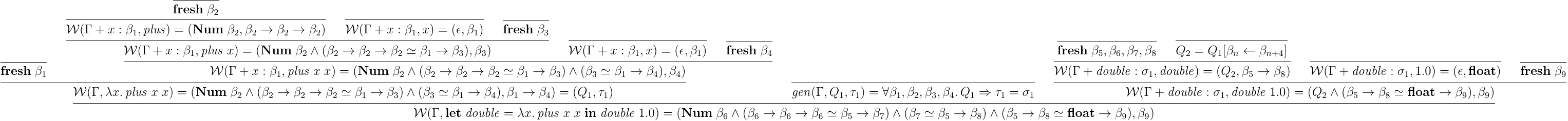
HM 型推論のアルゴリズム W に比べ，各所での単一化が起きずただ型の等価制約だけがどんどん増えていく．その等価制約に加え，必要な型制約も加えられ，最終的に変数を含む型と制約が生成される．これに対して，さらに $\mathrm{solv}(C, \mathbf{Num}\; \beta_6 \land (\beta_6 \to \beta_6 \to \beta_6 \simeq \beta_5 \to \beta_7) \land (\beta_7 \simeq \beta_5 \to \beta_8) \land (\beta_5 \to \beta_8 \simeq \mathbf{float} \to \beta_9)) = \theta$ により，$\theta(\beta_5) = \theta(\beta_6) = \theta(\beta_8) = \theta(\beta_9) = \mathbf{float}$， $\theta(\beta_7) = \mathbf{float} \to \mathbf{float}$ となるような置換 $\theta$ が生成されることになり，最終的に $\theta\beta_9 = \mathbf{float}$ が推論される型になる．このように，HM(X) では制約の生成が主な担当であり，その制約が妥当か検証し，制約から置換を生成することができれば，妥当な型が出力される．ただ，そのような制約解決をうまく定義するのはそれぞれの制約体系に任されることとなる．

制約解決

さて，HM(X) は制約を考慮した推論を，制約解決の方法が与えられた時に提供してくれる．最後にこの制約解決の方法についても言及しておこう．HM(X) 自体は基本これらの方法はパラメータとして与えられることが前提になっており，それを元に推論を提供してくれる体系なのだが，具体的に制約システムの方についても言及しておいた方がイメージがつきやすいだろう．

制約解決の役割は大きく2つある．1つは，型の等価制約からそれに合う置換を作成することだ．これは HM 推論での単一化に当たる．HM(X) では等価性が単純な構文的等価性の枠組みを超えることがあるかもしれない為，そのような体系にも耐えられるよう制約から置換を作成する．もう1つは制約の妥当性検証だ．つまり，推論された制約が満たされるべきものかを検証するということだ．この2つの役割を実現する為，制約解決はかなり段階を踏むことになる．

まず，制約を扱いやすいように原始制約の集合に変換する方法を用意しておく:

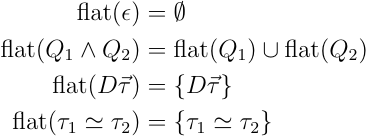
原始制約とは，$D \vec{\tau}$，$\tau_1 \simeq \tau_2$ のことで，もうそれ以上分解できないような制約のこと．今回は，この関数 $\mathrm{flat}$ により変換された集合に対して，書き換えシステムにより制約解決を行なっていく．書き換えシステムは，制約環境を取り，原始制約の集合をより単純な原始制約に変換するか，妥当でない原始制約が含まれていることを表す $\bot$ に書き換えを行う．具体的には以下のようなシステムにより制約解決を行える:

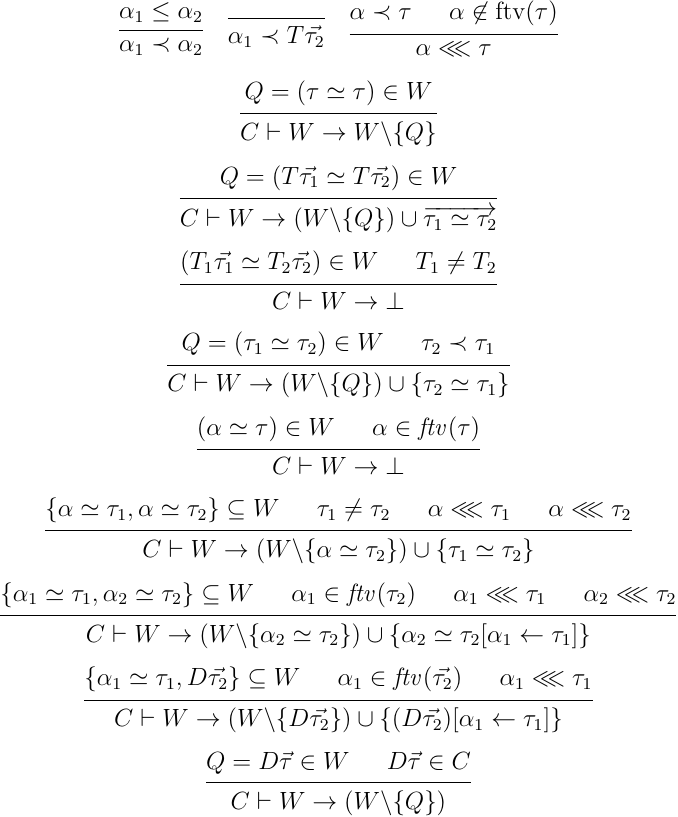
この制約解決システムは最終的に，

• 元の制約に現れる自由変数 $\alpha$ に対して，高々一つだけ代表的な型 $\tau$ を伴った等価制約 $\alpha \simeq \tau$
• 制約環境から解決できなかった制約 $D \vec{\tau} \not\in C$

だけを含む原始制約の集合に変換するか，制約が妥当でないことを表す $\bot$ に変換を行う．$\prec$ は等価制約を正規化するための関係で，何でもいいが変数に対しての全順序が提供された時，それを型全体に対して拡張する．与えられた原始制約の集合に含まれる全ての等価制約は，最初の3つの等価制約解決の規則と，4つ目の規則により，最終的にこの関係を遵守することになる．もう一つ，$\lll$ は正規化された等価制約であることを表す関係になっており，$\prec$ に加えて，妥当でない再帰的な等価制約でないことを表す．やはり，与えられた原始制約の集合に含まれる全ての等価制約は，最終的にこの関係を遵守するように変換される．残りの6から8番目の規則は最終的な置換を構成するための変数に紐づく型の単一化規則，最後の規則は制約環境からの制約の解決の規則になる．制約解決は，この書き換えシステムの正規系 [3] を元に，置換を構成することで定義される:

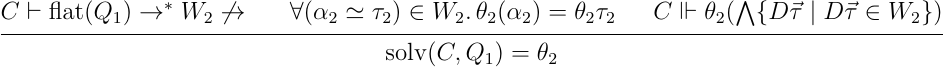
基本的に置換は書き換えにより生成された等価制約を元に構成される．ただ，等価制約には言及されない変数が存在することもある．そして，この変数が残っている状態だと制約解決がうまく行われないが，変数をうまく具体化すれば制約を満たすような状況が考えられる．例えば，$\mathbf{Num}\; \beta$ のような制約が書き換えの結果残ったとして，制約環境に $\mathbf{Num}\; \mathbf{float}$ のような制約が含まれていることを考える．この時，$\beta$ が置換に含まれなかったとしても，$\theta(\beta) = \mathbf{float}$ というような置換を加えれば制約を満たせる．このような制約を考慮したデフォルティングの余地を残すため，上記の定義では置換を具体的に構成していない．ただ，デフォルティングは諦めるという選択肢もあり，その場合は書き換えシステムのみで置換を構成できることになる．さて，この置換の構成を元に，最終的に以下のようにして制約を考慮した推論が行える:

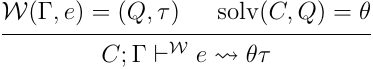
この時，推論を行なった型について，$C; \Gamma \vdash e: \theta\tau$ が成り立つ．例えば，

について，$C = \mathbf{Num}\; \mathbf{float}$，$\Gamma = 1.0: \mathbf{float} + \mathit{plus}: \forall \alpha\ldotp \mathbf{Num}\; \alpha \Rightarrow \alpha \to \alpha \to \alpha$ の下での型推論を考えてみる．上記で，第一段階の制約と型の生成の結果は，

であることが分かっている．後はこの生成された制約を書き換えシステムにより書き換えていく．なお，変数の順序は $n \leq m$ の時 $\beta_n \leq \beta_m$ と考える．この時，書き換えの過程は以下のようになる:

分かりやすいように各ステップで書き換え対象となっている原始制約を，赤で記している．書き換えの過程で型コンストラクタを含む等価制約がどんどん分解され，$\lll$ の関係を満たすよう整理されていき，最終的に単一化により型が具体化されていく様子が分かるだろう．この結果から，$\theta = [\beta_5 \leftarrow \mathbf{float}, \beta_6 \leftarrow \mathbf{float}, \beta_7 \leftarrow \mathbf{float} \to \mathbf{float}, \beta_8 \leftarrow \mathbf{float}, \beta_9 \leftarrow \mathbf{float}]$ のような置換が条件を満足することが分かり，最終的に $\theta\beta_9 = \mathbf{float}$ が推論結果として得られることになる．

制約解決と完全性

さて，HM(X) は基本的に制約の生成だけを担当し，その制約を解決する仕組みは別途制約体系として与える必要があった．上記では，その仕組みの具体例を紹介した．ところが，上記で与えた制約解決は実はかなり不完全である．つまり，本来制約解決を行えるようなものに関して，幾つか取りこぼしが生じるということだ．例えば，

のような型付について考えてみる．この型付が正しいことは，$C = \mathbf{Int} \simeq \mathbf{Int64}$， $\Gamma = f: \mathbf{Int} \to \mathbf{Int} + 1: \mathbf{Int64}$ と置いた時，以下のように確かめられる:

しかしこの式について，上記の型推論アルゴリズムを適用してみると，$\mathcal{W}(\Gamma, f\; 1) = (\mathbf{Int} \to \mathbf{Int} \simeq \mathbf{Int64} \to \beta, \beta)$ となり，$C \vdash \{\mathbf{Int} \to \mathbf{Int} \simeq \mathbf{Int64} \to \beta\} \to \{\mathbf{Int} \simeq \mathbf{Int64}, \mathbf{Int} \simeq \beta\} \to \bot$ となるため，型推論に失敗することになる．これは制約解決が，等価制約の解決について制約環境を参照しないことによる．

HM(X) は制約解決がうまく設計できれば，ある程度緩めた形ではあるが完全な推論を提供する．ところが，上記でも述べたとおり，HM(X) の主な役目は制約の生成であり，制約解決は何らかの形で別途与えられなければならず，完全さはその与えられた制約解決に大きく依存する．そして，この制約解決の設計こそが難関だったりする．制約解決をある程度計算時間を抑えつつ，完全性を保証するものにしたかったら，ある程度機能を絞るか，細かい制約の使用条件を課す必要が出てくる．これは各種言語苦労している部分で結構アドホックな対応になりがち．つまり，HM(X) は HM 推論の簡易な拡張としての立場を取りつつ，制約体系をパラメータとして様々な体系に適用できることを売りにしているわけだが，実際には制約体系をパラメータとして与えるように設計すること自体はそれほど簡易とは限らないわけだ．さらに，実は HM 推論を土台にしつつそのまま各体系に合わせて推論規則を拡張する方が素直にいく場合も多いというのが実情ではある．ま，ここら辺は，実用寄りの応用理論ではよく起こりがちのジレンマというやつだろう．

なお，今回あげた制約解決は

Dimitrios Vytiniotis, Simon Peyton Jones, Tom Schrijvers, and Martin Sulzmann. Outsidein(x): Modular type inference with local assumptions. Journal of Functional Programming, 21:333–412, 9 2011.

の一部を取り出したものとなっていて，この文献は Haskell の型推論の基礎理論となっているんだが，元文献の制約解決では type エイリアス，type family などを扱うため，もう少し強力な書き換えシステムと制約環境への追加条件などを紹介している．このような，HM(X) を基礎としつつ制約解決を頑張って設計し拡充していく方向性は良し悪しはあるものの，参考になる部分も多いだろう．ま，まさに参考実装としての側面では HM(X) は結構有用だ．ただ，上記の文献でも完全さはかなり諦めている．この辺は，実装としては完全さにこだわるよりも実用に耐えることが一般的には重視されるという面もあるが，HM(X) 自体の完全性を満たすように制約解決を設計する難しさがあるという面は否めないだろう．その辺は，HM(X) を基礎として型推論を実装する戦略を取る際は頭に入れておくのが良いと思う．

まとめ

というわけで，制約を考慮した HM 推論の拡張フレームワーク HM(X) の紹介だった．HM(X) は HM 推論を少しの工夫を入れることで制約という新たな要素に対応できるようにしている．ただ，HM(X) の本質は，HM 推論を制約生成も合わせて行うよう拡張している部分で，推論として完成するにはさらに生成された制約を解決し，置換をうまく生成するような仕組みが別途必要になる．そして，HM(X) 自体は割と簡易的な拡張に見えて，実際は制約解決の仕組みを作ることこそが難関という面がある．その為，HM(X) が提供している範囲のアルゴリズムだけでは，そのまま応用は難しいという側面もある．今回は，一応制約解決の方も具体的に構築例を示してみた．ま，何かの参考になればという感じ．

なお，Pottier 先生の ATTaPL の 10 章「The Essence of ML Type Inference」でも，HM(X) を具体的な制約システムの構成を踏まえて説明している．こちらは，HM 推論の説明から，HM(X) への拡張と具体的な制約システムの構成，ML の型推論実装に対する応用まで，ちゃんと各種形式化をしながら見ており，制約システムもかなり強力なものを構成している．こんな雑記事と違ってかなり参考になると思う (その分分量も多いが) ので，HM(X) に興味があればぜひ参照してみるのがいいんじゃないだろうか．

今回はこんな感じで．

[1]	なお，今回は分かりやすさと実装しやすさを優先し省略しているが，原文の規則では一般化で satisfiable という性質の導入を行い，制約含意でその性質が検証されるようにしている．この検証がない場合，絶対に満たされないような制約に対して一般化を行なってしまう可能性がある．個人的には別にそれでありだと思うし，制約の satisfiablity を考慮すると結構話がややこしくなるので今回はそこは検証しないようにしている．興味があれば題材の方を当たってもらうのが良いだろう．

[2]	HM(X) における本来の一般化は実はもう少し自由が与えられていて，型スキームに含める制約と環境に残す選択を分離できる．ただ，今回はアルゴリズムを単純にする為，そのような自由は許しておらず，全部の制約を型スキームに含めるようにしている．この辺は興味があれば題材の方をあたってもらうのが良いだろう．

[3]

正規系を考えるとなると，気になるのは停止性と合流性が成り立つかだが，今回のシステムは停止性は成り立つが残念ながら合流性は成り立たない．ある程度書き換え結果は一貫したものになること，妥当でない制約を含む場合は必ず $\bot$ に辿り着くことは保証できるが，完全に合流はせず書き換えによって最終的に得られる制約は変わる．そこら辺は実装依存ということになるだろう．合流性を保証する単純な方法は，書き換えシステムを決定的にすることだ．今回横着して，集合を使った書き換えを行なっているが，例えば原始制約の列に対して一番先頭から適用できる書き換え規則を適用していくというような規則を追加で入れれば，ある程度そこら辺の問題は解決できるだろう．今回は HM(X) の紹介という側面が強いのでそこまではやらず，とりあえず妥当な場合のみある程度一貫した結果が得られることだけで満足しておく．