Call Arity と融合変換

イータ展開と最適化

Haskell は知っての通り関数型プログラミング言語なので，息を吐くように関数を第1級として使うし，標準ライブラリに無数の高階関数がある．関数は全てカリー化されていて，部分適用も可能だ．ただ困ったことに Haskell は実用されており，これらの関数型プログラミング言語で常用されているテクニックで書かれたプログラムで，通常のプログラミング言語程度と妥当な勝負ができるぐらいのパフォーマンスを出さなければならない．しかし，カリー化と部分適用が気軽にできることは，実行マシンを考えると，かなりのハンデになる．

次のプログラムを例に考えてみる:

1
2
3
4

let
  g x y = x + y
  f = g 1
in f 2

このプログラムが何の変換もなされず，直接実行マシンに入力されるとする．単純に考えると全ての関数は一引数であると思って，関数適用を見つけたら引数を一つ一つ適用していけば実行できるわけだが，例えば今回の g のような多引数受け取らないと結果が返せない関数は単純に引数をキャプチャしたクロージャを生成するだけであり，かなり非効率になる．さすがに GHC ではそこまで安直なことはやっていなくて，一度に多引数の適用ができる場合中間オブジェクトを生成せずに関数適用を行う．現在の GHC では， eval/apply 方式と呼ばれる実行戦略を取っていて，関数の定義の形を見て引数の数が足りなければ部分適用を表す中間オブジェクトを生成し，引数の数が足りた時点で簡約を行う．今回の場合，大雑把には，

1. f 2 を評価しようとする．
2. f は g 1 を表すサンクとなっているので，引数の 2 をスタックに退避させて， f をまず評価する．
3. g は 2 引数関数なので， 1 だけでは足りないので，部分適用 g 1 を表す中間オブジェクトを生成し， f に再束縛する．
4. f に退避した 2 を適用すると，部分適用でキャプチャした 1 と合わせて引数が足りるので，その簡約結果 1 + 2 を返す．

のような動作をする．つまり，上のコードは中間オブジェクトを生成するため，その分のオーバーヘッドがかかる．ただこのようなコードは， Haskeller にとっては日常茶飯事であるわけなので，できるだけオーバーヘッドは無くしたいわけだ．実は，次のように少しコードを書き直すと，中間オブジェクトを生成する必要がなくなる:

1
2
3
4

let
  g x y = x + y
  f x = g 1 x
in f 2

f の定義に引数を一つ足しただけだ．この場合，

1. f 2 を評価しようとする．
2. f は 1 引数関数なので，引数の 2 をそのまま適用する．
3. 適用した結果の g 1 2 において， g は 2 引数関数なので，引数 1 ， 2 をそのまま適用する．
4. 簡約結果 1 + 2 を返す．

となる．一般に関数を表す式 f について， \x -> f x というようにラムダ抽象で包む形に変換する操作をイータ展開 (eta expansion) と呼び，今回は元のコードの f をイータ展開している．このようにイータ展開を行うことで，部分適用のための中間オブジェクト生成を抑制できる場合がある．

イータ展開は他にも，情報を付加することで let や ラムダ抽象のフローティング変換補助を行うことができたり，結構最適化の際に嬉しい．ただ，なんでもかんでもイータ展開すればいいかというとそうでもない．具体的には次のようなケース:

1
2
3
4

let
  g x y = x + y
  f = if expensiveExpression then g 1 else g 0
in f 2 + f 3

expensiveExpression は評価に時間のかかる式が入るとする．この場合， f をイータ展開すると， f 2 ， f 3 それぞれの呼び出しで expensiveExpression が計算されることになる．それに対し，イータ展開しない場合，サンクが評価された後2回目では計算が起こらない．

以上のようなことを考慮し，イータ展開していい引数の数を解析する手法が Call Arity 解析になる．

Call Arity 解析

Call Arity 解析が入る前も， GHC では似たような解析をしていてこれは Arity 解析と呼ばれていた． Call Arity 解析は従来の Arity 解析を Co-Call 解析と呼ばれる解析情報によって補助することで，より精度を上げようというものっぽい．具体的には以下のようなことを考える．

対象の構文として以下のものを考える．

今回の解析には型情報は必要ないので，考えるのは Core から型情報を抜いたようなもの．ただ， case とかはややこしい上にあまり本質ではないので，代わりに条件分岐を入れている． case の解析は条件分岐と同じことをすればいい．これに対し，変数集合を $V$ ，式の集合を $E$ として二つの相互に依存する解析関数

• Arity 解析: $A_n: E \to (V \rightharpoonup \mathbb{N})$
• Co-Call 解析: $C_n: E \to \mathcal{G}(V)$

を考える． $\rightharpoonup$ は部分関数， $\mathcal{G}(V)$ は $V$ を頂点とする無向グラフを表す． Arity 解析 $A_n(e)$ は受け取った式 $e$ に対して， $n$ 個引数が適用されたと仮定し，中の変数のアリティを解析した上でその対応表を返す． Co-Call 解析 $C_n(e)$ は受け取った式 $e$ に対して， $n$ 個引数が適用されたと仮定し，中の変数で同時に実行されるパスがある場合，辺が追加されたグラフを返す．なお自身への辺も許容され，辺がある場合2度以上使用される場合がある．例えば，

1
2
3

let g = \x y -> p x y in
let f = if s then g s else g t in
f z

というプログラム $e$ があった時，これを $A_0$ にかけると，結果は次のようになる:

また， $C_0(e)$ は以下のグラフを返す:

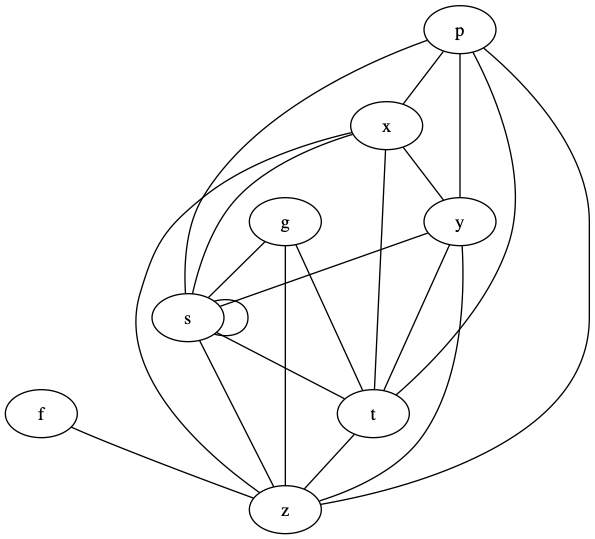
s が真の場合は f の中の条件分岐で g s の方に入り 2 回目が呼ばれることになるので，自身へのループを持つ．それ以外の変数は 1 回しか使用されない．この自身へのループを持つかは重要で，これがある場合イータ展開すると本来サンク一回の評価で良かったものを複数回評価してしまうことになる．また g や f の内部の変数は，それぞれの関数が呼ばれると使用されるので， g や f に紐づく変数と紐づくことになる．イメージとしてはこんな感じ．

解析は再帰的に定義される．詳細は論文の方にまとまってるので，そちらを参照してくれって感じ．一応，条件分岐とラムダ抽象， let だけ紹介しておく．

条件分岐

$$e = \mathop{\mathbf{if}} e_1 \mathop{\mathbf{then}} e_2 \mathop{\mathbf{else}} e_3$$

について，

$$A_n(e) = A_0(e_1) \sqcup A_n(e_2) \sqcup A_n(e_3)$$

$$C_n(e) = C_0(e_1) \cup C_n(e_2) \cup C_n(e_3) \cup (\mathit{fv}(e_1) \times (\mathit{fv}(e_2) \cup \mathit{fv}(e_3)))$$

と定義する．ここで， $\mathit{fv}(e)$ は $e$ の中の自由変数の集合，他の演算子は以下のようになる:

$$X_1 \sqcup X_2 = \{x \mapsto n_{\mathrm{min}} \mid x \in \mathrm{dom}(X_1 \cup X_2), n_{\mathrm{min}} = \min \{n \mid x \mapsto n \in X_1 \cup X_2\}\}$$

$$V_1 \times V_2 = \{v_1 \mathrel{\text{--}} v_2 \mid v_1 \in V_1, v_2 \in V_2\}$$

Arity 解析の方は，まず $e_1$ は $e$ に何個引数が適用されようが関係なくアリティ 0 になる． $e_2$ と $e_3$ は， $e_1$ の計算結果によって， $e$ の引数がそのまま適用されることになる． Co-Call 解析の方は $e_1$ の結果によって $e_2$ ， $e_3$ どちらかが実行されることになるので，そのどちらかの実行を表す辺を追加するだけ．

ラムダ抽象

$$e = \text{\texttt{\textbackslash}} x_1 \cdots x_m \mathbin{\text{\texttt{->}}} e_1$$

について，

$$A_n(e) = \left\{\begin{array}{ll} A_{n'}(e_1) &(n = n' + m) \\ A_0(e_1) &(n < m) \end{array}\right.$$

$$C_n(e) = \left\{\begin{array}{ll} C_{n'}(e_1) &(n = n' + m) \\ \mathit{fv}(e_1) \times \mathit{fv}(e_1) &(n < m) \end{array}\right.$$

ラムダ抽象は引数が足りる場合その数分引数の数を差し引いて中の式を解析する．足りない場合がポイントで，この場合ラムダ抽象は返り値の部分値として使われるか他の関数の引数として使われ，その後どう使われるか分からない．そしてもちろん，複数回使用されることもあり得る．それ以上の解析はここではできない前提とし，複数回使用されることを想定して Co-Call 解析では $e_1$ で使用される変数同士を結びつけている．また Arity 解析も $e_1$ を展開しない前提で解析をしていく．

let

$$e = \mathop{\mathbf{let}} x \mathbin{\text{\texttt{=}}} e_1 \mathop{\mathbf{in}} e_2$$

について，

$$A_n(e) = A_{n_x}(e_1) \sqcup A_n(e_2)$$

$$C_n(e) = C_{\mathrm{rhs}} \cup C_n(e_2) \cup (\mathit{fv}(e_1) \times \{v \mid v \mathrel{\text{--}} x \in C_n(e_2)\})$$

と定義する．ここで， $n_x$ と $C_{\mathrm{rhs}}$ は以下のように定義する:

$$n_x = \left\{\begin{array}{ll} 0 &(x \mathrel{\text{--}} x \in C_n(e_2), \text{$e_1$ not in HNF}) \\ A_n(e_2)(x) &(\text{otherwise}) \end{array}\right.$$

$$C_{\mathrm{rhs}} = \left\{\begin{array}{ll} C_{n_x}(e_1) &(x \mathrel{\text{--}} x \not\in C_n(e_2) \lor n_x = 0) \\ \mathit{fv}(e_1) \times \mathit{fv}(e_1) &(\text{otherwise}) \end{array}\right.$$

ちょっと今までのものに比べ複雑だが，順を追って見ていく．

Arity 解析の方は $x$ のアリティを $e_2$ から解析した結果を $n_x$ として，それを元に $e_1$ の解析をした上で $e_2$ の結果とくっつける．単純には $n_x$ は $A_n(e_2)(x)$ で得られるわけだけど，一番最初の話を思い出してもらうと， $e_2$ 中で $x$ が複数回計算され，しかも $e_1$ が HNF ではない場合，イータ展開すると一回で済んだサンクの計算を複数回行ってしまうことになる．そこで， $e_2$ の Co-Call 解析の結果から $x$ が複数回使用されることが分かり， $e_1$ が HNF でない場合はイータ展開を抑制するためアリティを 0 にする．

Co-Call 解析の方は，まず $e_2$ で $x$ の使用がたかだか一回の場合または $e_1$ をイータ展開しないと決めた場合 $e_1$ を　$x$ のアリティの元解析する．それ以外の場合 $x$ が複数回使用されるとして $e_1$ で使用される変数同士を結びつける．それが $C_{\mathit{rhs}}$ の結果となる．後はそれと $e_2$ の解析結果をくっつけ，さらに $e_2$ で $x$ が評価されるパスで評価される変数は $x$ の内部で使われてる変数，つまり $e_1$ で評価される変数と同時に使用されるということでもあるので，その変数同士も結びつけるということをしている．

後は元論文のテーブルを参照してくれ．以上のことが分かれば，後は読めると思う．元論文だと正当性証明が課題として書いてあるが，その後 証明 もされてるっぽい．

foldl と Call Arity

ところで，最近の GHC では foldl は foldr で定義されている．これは融合変換を foldl にも適用するためで，実は Call Arity 解析の搭載はこの定義が強い動機になっている．具体的にどういう定義になっているかというと，以下の通り [1] :

1
2

foldl :: (b -> a -> b) -> b -> [a] -> b
foldl k z0 xs = foldr (\x fn z -> fn (k z x)) id xs z0

このコードだとちょっと混乱するかもだが，次のように書き直すと分かりやすいかもしれない:

1
2

foldl :: forall a b. (b -> a -> b) -> b -> [a] -> b
foldl k z0 xs = (foldr (\x fn -> fn . (\z -> k z x)) id xs :: b -> b) z0

要は左畳み込みで返り値を作っていく代わりに，初期値を受け取って返り値を返す関数を関数合成により右畳み込みしていくだけ．で，抽象部分のアリティを明示して合成を明示しないで書くと上の定義が出てくる．ここで重要なのが，アキュムレータが関数になっている点．つまり，関数を再帰的に構築していくことになる点だ．

例えば sum の定義は，

1
2

sum :: Num a => [a] -> a
sum = foldl (+) 0

となる訳だけど，これは，

1

sum xs = foldr (\x fn z -> fn (z + x)) id xs 0

と等しくなる．これを次の生産者とくっつけたものを考えてみる:

1

sum (filter even (enumFromTo 0 10))

リスト内包表記で書くと，これは次のようなものと同じになる:

1

sum [x | x <- [0..10], even x]

それぞれの関数は foldr/build の融合変換が発火するようになっていて，だいたい次のような関数に落ち着く:

1
2
3
4
5

go 0 0 where
  go :: Num a => a -> (a -> a)
  go x =
    let fn = if x == 10 then id else go (x + 1)
    in if even x then \z -> fn (z + x) else fn

これはリストの中間データを削減してはいるものの，それに相当するクロージャを都度生成してしまうためあまりよろしくない．しかしこの場合， Call Arity 解析により，より良い形に変換できる． fn のアリティを 1 に， go のアリティを 2 にすることが可能なことが分かるので，以下のイータ展開を行うことができる:

1
2
3
4

go 0 0 where
  go x z =
    (let fn z' = (if x == 10 then id else go (x + 1)) z'
    in if even x then \z -> fn (z + x) else fn) z

後はベータ変換とインライン展開により，以下の形に持っていける:

1
2
3
4

go 0 0 where
  go x z =
    let fn z' = if x == 10 then z' else go (x + 1) z'
    in if even x then fn (z + x) else fn z

もちろん fn をラムダリフティングで外に出すことやインライン展開することも可能で，そうなると一切クロージャ生成を行わないコードができ，しかも単純な末尾呼び出しの形になっている．さらに，引数の z に関する正格性解析により，アキュムレータを正格にぶん回すことができ，元のに比べかなりの効率化が見込める．

このように Call Arity 解析により，関数をアキュムレータとして持つような foldr を使ったプログラムを，融合変換が発火した後にさらに改善することが可能になるケースがある．特に， foldl を定義そのままで最適化をかけることができるのは大きいだろう．

oneShot 関数

さて Call Arity 解析は， Co-Call 解析により複数回使用されるかの情報を元に Arity 解析を補助することで，うまくイータ展開すべき部分と抑制すべき部分を切り分けることができる．ただラムダ抽象の解析で見た通り，ラムダ抽象のまま残ってしまってその後関数に適用される式などは，その中身が複数回使用される前提になってしまう．

一応 GHC では， GHC.Magic.oneShot :: a -> a という関数が提供されていて，こいつを使うとその値が単一使用であることをコンパイラに教えることができる．例えば，

1
2

let g = ...
in f (\x -> g x)

というプログラムにおいて，本来の Call Arity 解析では $g$ は複数回使用だと判定されてしまうため HNF でない場合イータ展開が抑制される．しかし， f が引数の関数を一回しか使わないと分かっていれば，

1
2

let g = ...
in f (oneShot \x -> g x)

と書くことで g のイータ展開を支援できる．この例だとあまり嬉しみが分からないが， oneShot は以下のようにも使える．

1

foldl k z0 xs = foldr (\x fn -> oneShot (\z -> fn (k z x))) id xs z0

これは実際の foldl の定義．注目したいのはラムダの中で oneShot を書いてる点． foldr に渡す関数はリストの長さ分使用されるが，その中のアキュムレータとして返す関数は，各リストの要素と前のアキュムレータに対して一度きりの使用となる．

実際の世界では Call Arity 解析だけでうまくいかないケースもあり， foldl も生産者によっては融合変換の結果微妙な形になってしまうこともある． oneShot をつけておくとその補助情報で Call Arity 解析がうまくいくようになる場合もある．なので，汎用的な関数で Call Arity 解析によるイータ展開を期待するなら oneShot をつけれるところは付けておくと無難だろう．

まとめ

というわけで， foldl が foldr で定義されるようになった裏で，新たに搭載された解析手法を紹介した．さらに GHC 8 系では，従来の正格性解析を強化した Demand Analysis に切り替わったり， Core に join point が入ったりと内部は大きく変わっている．なお， Demand Analysis について知ってる人は， Co-Call 解析から取れる情報が Demand Analysis と被ってることに気づくと思う．実際その部分を統一化する話もあって， https://icfp17.sigplan.org/details/hiw-2017/14/Demand-Analysis-vs-Call-Arity でそれについて触れられてるんだけど，この話が結局どうなったのか知らない．将来的にこれも取り入れられたりするんだろうか？

ただ Call Arity は実際うまく入らない場合もあり， oneShot のような補助情報を別途つける必要も生じる．ここから foldl で書けるなら明示的にループを書くよりこいつらを使った方が，より効率よくなる場合が多いということだ．これは foldl' でも同じなので，正格性解析が入るかどうかを気にしたくないなら foldl' を使っていれば融合変換が入り，インライン展開後もうまくワンショットラムダでぶん回す再帰に変換されるようになる．

あんまり詳しくなかった解析なので，これでちょっとは融合変換のパフォーマンス予測がしやすくなったんだろうか．正直融合変換周り，元のコードから形が変わりすぎて Core 出力読めねえんだよなあ．こちらからは以上です．