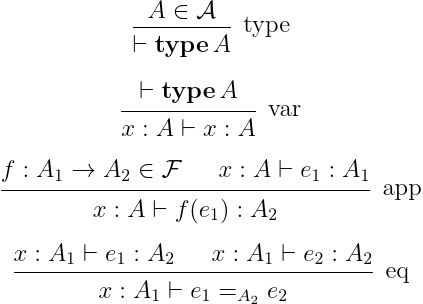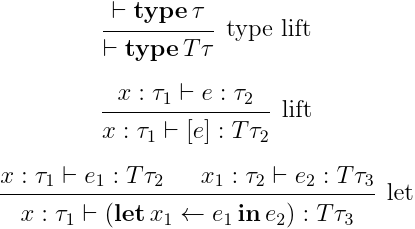Graded Monad とエフェクト

モナドとエフェクト

まず基本的なやつから．以下の構造は一対一の対応を持つ．

クライスリトリプル (Kleisli triple)

圏 $C$ 上のクライスリトリプルとは，以下の要素の組 $(T, \eta = \prod_{A \in |C|} \eta_A, -^*)$ で，

• 写像 $T: |C| \to |C|$
• 任意の $A \in |C|$ に対して $\eta_A \in \mathrm{Hom}_C(A, T A)$
• 任意の $A, B \in |C|$ についての， $f \in \mathrm{Hom}_C(A, T B)$ に対する操作 $f^* \in \mathrm{Hom}_C(T A, T B)$

以下の条件を満たすもの

• 任意の $A \in |C|$ について， $\eta_A^* = id_{T A}$
• 任意の $f \in \mathrm{Hom}_C(A, T B)$ について， $\eta_A; f^* = f$
• 任意の $f \in \mathrm{Hom}_C(A, T B)$ ， $g \in \mathrm{Hom}_C(B, T C)$ について， $f^*; g^* = (f; g)^*$

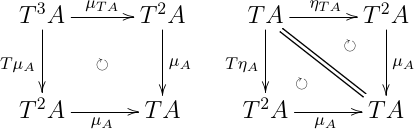
モナド (monad)

圏 $C$ 上のモナドとは，以下の要素の組 $(T, \eta, \mu)$ で，

• 関手 $T: C \to C$
• 自然変換 $\eta: \mathrm{Id} \Rightarrow T: C \to C$
• 自然変換 $\mu: T^2 \Rightarrow T: C \to C$

任意の $A \in |C|$ について，以下を満たすもの

対応は以下のように作る．

クライスリトリプルからモナド

クライスリトリプル $(T, \eta, -^*)$ に対して，モナド $(T', \eta', \mu')$ は以下のように作る．

• $T': |C| \to |C|; A \mapsto T A$ ， $T': \mathrm{Hom}_C(A, B) \to \mathrm{Hom}_C(T' A, T' B); f \mapsto (f; \eta_B)^*$
• $\eta'_A = \eta_A$
• $\mu'_A = (\mathrm{id}_{T A})^*$

これがモナドであることの証明はめんどくさいのでやらないけど，やればできる．

モナドからクライスリトリプル

モナド $(T, \eta, \mu)$ に対して，クライスリトリプル $(T', \eta', -^*)$ は以下のように作る．

• $T'; A \mapsto T A$
• $\eta'_A = \eta_A$
• $(A \xrightarrow{f} T B)^* = (T f); \mu_B$

こっちもクライスリトリプルであることの証明は省略する．

この作り方は，互いに同型になっていることも確かめれば分かる．というわけで，クライスリトリプルは実質モナド．モナドはコヒーレンス規則が綺麗な形をしていて分かりやすいわけだけど，クライスリトリプルの形の方がプログラム意味論を考える上では便利．

さてこいつらがプログラム意味論とどう関わってくるかだけど，例えば以下の構文を持つ簡単な言語に対して意味論を与えることを考えたい．考える言語は，

• 型がある． (type)
• 型がついた変数がある． (var)
• 関数適用ができる． (app)
• 式の等価性が判定できる． (eq)

みたいな感じ．だいたい次のようなものを想像してくれ．

で，こいつらには圏 $C$ 上のいい感じの categorical な意味論が与えられていて，

• 型 $A \in \mathcal{A}$ の解釈 $⟦A⟧$ は， $|C|$ の中で与えられる．
• 関数 $f: A_1 \to A_2 \in \mathcal{F}$ の解釈 $⟦f⟧$ は， $\mathrm{Hom}_C(⟦A_1⟧, ⟦A_2⟧)$ の中で与えられる．
• アサーション $\vdash$ は， $C$ の射の等価性判定に対応する．

という感じになっていて，上の規則には，

• var: $\mathrm{id}_{⟦A⟧}$
• app: $⟦x: A \vdash e_1: A_1⟧; ⟦f⟧$
• eq: $⟦x: A_1 \vdash e_1: A_2⟧ = ⟦x: A_1 \vdash e_2: A_2⟧$

という解釈がついてると想定する．さて現実の言語では，もうちょっと高尚な要素が欲しい場合がある．例えば，計算途中で例外を投げる，状態を更新しながら計算を行うとかだ．これを，上の意味論を流用しながら組み込めないかと考えた時，クライスリトリプルが登場する．例外を例にすると，例外の集合を $E$ とした時，次のクライスリトリプル $(T, \eta, -^*)$ を考える [1] ．

• $T; A \mapsto A + E$
• $\eta_A = \mathrm{inj}_A$
• $(A \xrightarrow{f} B + E)^*(\mathrm{inj}_A(x)) = f(x)$ ， $(A \xrightarrow{f} B + E)^*(\mathrm{inj}_E(x)) = \mathrm{inj}_E(x)$

こいつを使って，次の構文を追加してさっきの意味論を拡張する．

で，さっきの要素の解釈については特に変えないで，新たな要素について，

• type lift: $T ⟦\tau⟧$
• lift: $⟦x: \tau_1 \vdash e: \tau_2⟧; \eta_{⟦\tau_2⟧}$
• let: $⟦x: \tau_1 \vdash e_1: T \tau_2⟧; ⟦x_1: \tau_2 \vdash e_2: T \tau_3⟧^*$

という解釈を入れる．さっき考えた例外のクライスリトリプルで，こいつらがどういう意味に当たるかを考えてみると，

• lift は，単純に例外の起きなかった計算結果を埋め込む．
• let は，例外が起きるかもしれない計算を実行し，例外が起きたら次はスルー，起きなかったら計算結果を次に渡して次を実行する．

という操作に当たる．で．クライスリトリプルの条件は，

というコヒーレンスに対応している．クライスリトリプルの各要素が，それぞれの構文の解釈を担うのはかなり綺麗だ．で，上のコヒーレンスが成り立つので，元の言語の意味論で equational reasoning がいい感じの性質を持ったまま作れるなら，こちら用にも拡張できる．後は，言語の機能に合わせていい感じのクライスリトリプルを作ってやって，表層言語にいい感じの意味論を与えてやれば，それらを元に言語機能に合わせた意味論を構成してやることができるというわけだ．

この表層言語から切り離された，モナド (クライスリトリプル) の部分が，いわゆる計算作用 (computational effect) と呼ばれる部分だ．

モナドは lax monoidal functor

さて，モナドによりエフェクトと表層言語の分離がしやすくなるわけだけど，この分野ではもう一つ大きな需要があったらしく，それがエフェクト解析と呼ばれる分野らしい．今までは，エフェクトと表層言語両方用意する話をしてきたわけだけど，逆に表層言語だけ見てエフェクトの近似が出来ないか，特にどういう場所でどういうエフェクトが起こるかをもうちょっと詳細に見れないかという研究があったっぽい．で，このエフェクトの類推を型システムに載せられないかという話があり，それが今日のエフェクトシステムにつながる．

で，起こりうるエフェクトの種類が限られていて，それに名前がつけられる場合に，ある式に対して型とともに起こりうるエフェクトが追加された情報のジャッジメントができないだろうかというのが考えられた．そして，それを上のモナドを使った意味論の形で表現できないかというわけだ．イメージとしては，以下の感じ．

$f: \tau_1 \xrightarrow{\epsilon} \tau_2$ は関数 $f$ を実行するとエフェクト $\epsilon$ が発生すると読む． $1$ は単位的なエフェクトで，エフェクト同士には二項演算がある．また，エフェクト同士には順序があって，その順序に対してアップキャストルールがある．この言語に対して，モナドの意味論と同じように categorical な意味論のある表層言語から意味論を構築できないか考えたい．無理やりモナドによる意味論と同じ形で当てはめてみると，以下のようなものが出来上がる．

• effect: $⟦-⟧_{\mathcal{E}}$ は，以下を満たす．
  • $⟦1⟧_{\mathcal{E}} = 1$
  • $⟦\epsilon_1 \cdot \epsilon_2⟧_{\mathcal{E}} = ⟦\epsilon_1⟧_{\mathcal{E}} \cdot ⟦\epsilon_2⟧_{\mathcal{E}}$
• type lift: $T ⟦\epsilon⟧_{\mathcal{E}} ⟦\tau⟧$
• lift: $⟦x: \tau_1 \vdash e: \tau_2⟧; \eta_{⟦\tau_2⟧}: ⟦\tau_1⟧ \to T 1 ⟦\tau_2⟧$
• effectful app: $⟦x: \tau \vdash e: \tau_1⟧; ⟦\tau_1⟧ \xrightarrow{⟦f⟧} T ⟦\epsilon⟧_{\mathcal{E}} ⟦\tau_2⟧: ⟦\tau⟧ \to T ⟦\epsilon⟧_{\mathcal{E}} ⟦\tau_2⟧$
• let: $⟦x: \tau_1 \vdash e_1: T \epsilon_1 \tau_2⟧; ⟦x: \tau_2 \vdash e_2: T \epsilon_2 \tau_3⟧^*: ⟦\tau_1⟧ \to T ⟦\epsilon_1 \cdot \epsilon_2⟧_{\mathcal{E}} ⟦\tau_3⟧ = ⟦x: \tau_1 \vdash e_1: T \epsilon_1 \tau_2⟧; T ⟦\epsilon_1⟧_{\mathcal{E}} ⟦x: \tau_2 \vdash e_2: T \epsilon_2 \tau_3⟧; \mu^{\epsilon_1, \epsilon_2}_{⟦\tau_3⟧}$
• effect ord: $⟦\vdash \epsilon_1 \sqsubseteq \epsilon_2⟧ = ⟦\epsilon_1⟧_{\mathcal{E}} \sqsubseteq ⟦\epsilon_2⟧_{\mathcal{E}}$
• cast: $⟦x: \tau_1 \vdash e: T \epsilon_1 \tau_2⟧; T (⟦\vdash \epsilon_1 \sqsubseteq \epsilon_2⟧) ⟦\tau_2⟧: ⟦\tau_1⟧ \to T ⟦\epsilon_2⟧_{\mathcal{E}} ⟦\tau_2⟧$

問題は，以下の 4 つの要素がどういうものになるかということ．

• エフェクトの解釈 $⟦-⟧_{\mathcal{E}}$
• エフェクトを考慮した関手っぽい何か $T \epsilon: C \to C$ ， $T (\epsilon_1 \sqsubseteq \epsilon_2): T \epsilon_1 \Rightarrow T \epsilon_2: C \to C$
• 自然変換 $\eta: \mathrm{Id} \implies T 1: C \to C$
• 自然変換 $\mu^{\epsilon_1, \epsilon_2}: T \epsilon_1; T \epsilon_2 \Rightarrow T (\epsilon_1 \cdot \epsilon_2): C \to C$

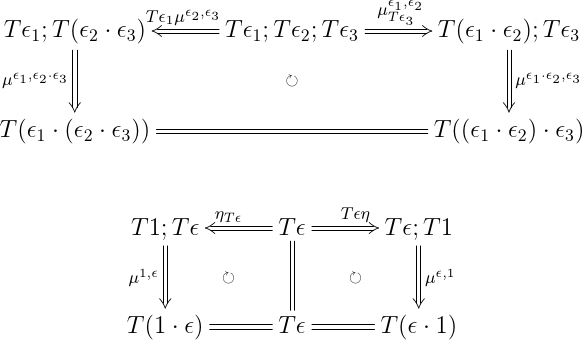
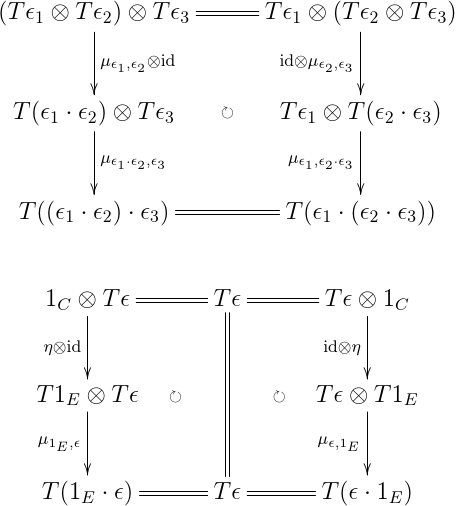
これらの要素は，もちろん何でもいいってわけではなく， equational reasoning を構築するため，コヒーレンスを満たす必要がある．コヒーレンスの形は，モナドから推定するなら，以下のような形になりそうだ．

で，ここまでくると二項演算の性質も決まってきて，

• $\epsilon_1 \cdot (\epsilon_2 \cdot \epsilon_3) = (\epsilon_1 \cdot \epsilon_2) \cdot \epsilon_3$
• $1 \cdot \epsilon = \epsilon = \epsilon \cdot 1$

となる．つまりは，モノイドというわけ．順序と合わせると，エフェクトの解釈領域をある構造で一般化できる．それは， monoidal category だ． monoidal category とは，以下の要素の組 [2]．

• 圏 $C$
• テンソル積: $\otimes: C \times C \to C$
• 単位対象: $I \in |C|$

で，以下を満たすもの．

• 任意の $A_1, A_2, A_3 \in |C|$ に対して， $(A_1 \otimes A_2) \otimes A_3 = A_1 \otimes (A_2 \otimes A_3)$
• 任意の $A \in |C|$ に対して， $A \otimes I = A = I \otimes A$

そうすると，エフェクトを考慮したモナド的な何かは， lax monoidal functor として定式化できる．monoidal category $(E, \cdot, 1_E)$ から $(C, \otimes, 1_C)$ への lax monoidal functor とは，以下の要素の組．

• 関手: $T: E \to C$
• 射: $\eta: 1_C \to T 1_E$
• 自然変換: $\mu: T - \mathbin{\otimes} T - \implies T (- \cdot -): E \times E \to C$

で，以下を満たすもの．

$C$ 上のモナドは， 1 から自己関手圏 $([C, C], ;, \mathrm{Id})$ [3] への lax monoidal functor に一致する．いわゆる，自己関手圏でのモノイド対象というやつで，一般に monoidal category のモノイド対象とは 1 からの lax monoidal functor のこと．エフェクトを考慮した意味論を与える時に考えていたものは，モナドの一般化で，エフェクトの解釈領域である monoidal category $E$ からいい感じの意味論が与えられている圏 $C$ を元にした自己関手圏 $[C, C]$ への lax monoidal functor になる．で，この場合の lax monoidal functor のコヒーレンスを簡略したものが，モナドから無理やり導出したコヒーレンス則になる．

graded monad とエフェクトシステム

この monoidal category から自己関手圏への lax monoidal functor のことを graded monad というらしい．またの名を parametric monad で， monad において 1 から自己関手圏の lax monoidal functor だったものを 1 の部分を任意の monoidal category にしてパラメータとしてとれるようにしたということだ．

実際には拡張した意味論を考える際には，エフェクトが monoidal category まで弱めるとちょっと不便なことがあって，今回エフェクトの射は順序づけに使うだけなので，対象間に複数射が伸びてるみたいな必要はない．なので， monoidal category をさらに制限して， preorder (反射推移的な二項関係) と monoid がある構造 preordered monoid を採用するっぽい．で，この preoredered monoid から $[C, C]$ への lax monoidal functor を使って，モナドの時と同じように意味論の自然な拡張を行うという話になる．

で，表層言語から (preordered monoid に制限した) graded monad を使って拡張した言語をエフェクトシステムと呼ぶらしい．広義的には，前に紹介したエフェクトの細かい推定ができる型システムのことかしら？

例えば，以下のような graded monad $T: E \to [C,C]$ を考えてみる．

ここで， $S: E \to C$ は関手．こいつは state モナドの graded monad 版． $\eta: \mathrm{Id} \Rightarrow T 1$ は，

なことから，エンドの一意な射を持ってくることができる． $\mu^{\epsilon_1,\epsilon_2}: T \epsilon_1; T \epsilon_2 \Rightarrow T (\epsilon_1 \cdot \epsilon_2)$ は，エンドと冪の射を使って，

という射が構成できるので，やはりエンドの一意な射を持ってくることができる．

例えば， $C = \mathrm{Set}$ ， $E = \mathcal{P}(\mathbb{N})$ ， $S = (-) \rightharpoonup \mathbb{N}$ (射に対しては，単に定義域を広げる) を考えてみると，

となり，自然数でアクセスできるメモリを状態とする state モナドとほぼ同じになることが分かる．異なるのは状態の型が変わっていく可能性があることで，今まで使用したメモリ番地のみがエフェクトとして現れる．こんな感じで，モナドにしてしまうと常に同じエフェクトの見積もりになるところを，もう少し細かく見ることができるようになるのがエフェクトシステムの特徴っぽい？

ところで， graded monad はパラメータを固定してもモナドにならない場合があることには注意．上の例だと， $I$ を固定すればモナドが作れるんだけど，一般に monoid は $\epsilon \cdot \epsilon = \epsilon$ とは限らないので， $\mu^{\epsilon,\epsilon}: T \epsilon; T \epsilon \Rightarrow T (\epsilon \cdot \epsilon)$ がモナドの $\mu$ に一致しない．ただ， $1 \cdot 1 = 1$ なので， $T 1$ はモナドになる．

まとめ

エフェクトシステム勉強会からだいぶ経ってしまったけど，とりあえず調べたことを簡単にまとめた．お気持ちが何となく分かったので，結構論文が読めて楽しい．

エフェクトシステムと聞くと algebraic effect とかプログラミング機能寄りの話にいきがちだったけど，そもそも新たな型システムとして，モナドによる意味論をもうちょっとやれる部分があるやろという感じの話なんだなというのが分かってきた (Plotkin 大先生によるエフェクトシステム勉強会の方，行けてない勢並の感想) ．

indexed monad とかも実際には，エフェクトシステムの方やりたいやつもいくつかありそうやなみたいなことも思った． algebraic effect の意味論を考える場合，また違った話になるっぽいけど，

[1]	何の断りもなく直和が出てきてるが，もちろん直和が $C$ にあるとは限らない．ただ，ここではいい感じの意味論がある前提で話を進めているので，直和もあるという前提で話を進めている．以降も $C$ にいい感じの性質を断りなしに要求している場合があるが，ここではそういう前提を暗黙のうちに置いてるのねと思ってくれ．

[2]	通常の monoidal category は，他に 3 つの自然同型が付随していて，結合律を弱める $\alpha_{A, B, C}: (A \otimes B) \otimes C \simeq A \otimes (B \otimes C)$ ，単位元律を弱める $\lambda_A: I \otimes A \simeq A$ ， $\rho_A: A \otimes I \simeq A$ を設け，いい感じのコヒーレンス規則を設定する．今回の定義はこれらが恒等変換となっている場合で， strict monoidal category と呼ばれる．

[3]	通常の自己関手圏は $\circ$ をテンソル積に据えるけど，今回は書きやすさのため，その flip 版を用いている．言ってることは変わらないので，気にしないでくれ．