http://ziphil.com/diary/application/26.html を読んでるとき,まとめたことを記事として残しておこうと思った.
参考文献は,
Barr, M. (1992). Algebraically compact functors. Journal of Pure and Applied Algebra, 82(3), 211–231. https://doi.org/10.1016/0022-4049(92)90169-G
なお以降考える圏は,特に断りのない限り, initial object 0 及び terminal object 1 が存在し,chain cocomplete (chain に対する図式が colimit を持つ) で cochain complete (cochain に対する図式が limit を持つ) であるとする.
F-algebra と F-coalgebra
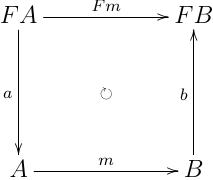
圏 C,自己関手 F:C→C において,F-algebra は,射 FXaX のこと.で,F-algebra 同士の射を以下の図式を可換にする射 h (F-algebra 準同型射と呼ぶ)
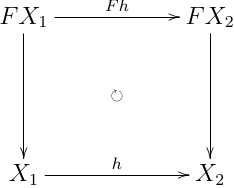
とすると, F-algebra による圏 AlgC(F) を構成できる.この圏で initial object が存在したとき,それを initial F-algebra と呼ぶ.その双対をそれぞれ F-coalgebra , CoAlgC(F) ,terminal F-coalgebra と呼ぶ.
ところで, initial algebra FAaA において, FA∼A であることが知られている.
- 定理. (Lambek's Theorem)
自己関手 F:C→C において,initial F-algebra FAaA があるとする.この時,a は同型射.
証明:
以下の図式は可換:
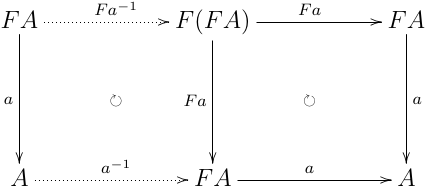
よって, initial algebra からの射の一意性から,a−1;a=id.さらに,左の図式だけ考えると a;a−1=Fa−1;Fa=F(a−1;a)=Fid=id より,a は同型射になる.
双対的に, terminal F-coalgebra についても同型であることが示せる.ところで, initial / terminal object から initial algebra / terminal coalgebra を構成できる場合がある.それは,initial / terminal sequence が途中で同型の列になる場合である.
- 定義. (initial / terminal F-sequence)
以下の順序数で添字づけられた図式を (ordinal) initial F-sequence と呼ぶ.
0∃!fF0FfF20F2f⋯Fω0Fωf⋯Fα0Fαf⋯
なお,任意の順序数 α,β≤α について,Fα0,fαβ:Fβ0→Fα0 を,以下のように定める:
- α=0 の時
- F00=0,f00=id
- α=1 の時
F10=F0,
f1β={fid(β=0)(β=α=1)
- α が極限順序数の時
- (fαβ:Fβ0→Fα0)β<α は chain (Fβ0)β<α の colimit で定める.また,fαα=id
- α=γ+1 で,γ が極限順序数の時
- Fα0=F(Fγ0) とする.この時,β<γ に対して,fαβ=fβ+1β;Ffγβ とおくと,(fαβ:Fβ0→Fα)β<γ は cocone になるので一意射 fαγ が存在する.これらで β≤γ については fαβ を定める.また,fαα=id
- α=γ+2 と書ける時 (つまり,上記以外の場合)
Fα=F(Fγ+10),
fαβ={fγ+1β;Ffγ+1γid(β≤γ+1)(β=α)
この定義が well-defined であること,以下が成り立つことは帰納法により容易に示せる:
- Fα+10=F(Fα0)
- fα+1β+1=Ffαβ
- fαα=id
- β≤γ≤α の時,fγβ;fαγ=fαβ
また,以下の順序数で添字づけられた反変図式を (ordinal) terminal F-sequence と呼ぶ.
1∃!gF1FgF21F2g⋯Fω1Fωg⋯Fα1Fαg⋯
この時,Fα1,gαβ:Fβ1→Fα1 を initial sequence と双対的に定める.
initial / terminal sequence が途中で同型の列になる時,その列は停止するという.
- 定義. (initial / terminal sequence の停止性)
- fα+1α が同型になる時,initial sequence は α で停止するという.双対的に,gαα+1 が同型になる時,terminal sequence は α で停止するという.
なお,関手は同型を保存するので α で停止する initial sequence は α 以降の射が全て同型射になる.ところで,initial sequence の停止性の条件に,次のものがある.
- 命題.
ある α,β<α で,fαβ が同型射ならば,fβ+1β は同型射
証明:
Ffαβ=fα+1β+1=fαβ+1;fα+1α
より,以下の図式が可換:
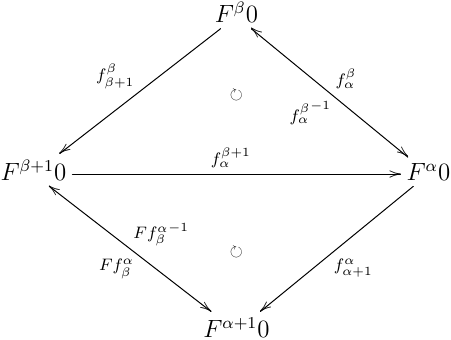
この時,fαβ+1 は同型射になり,よって fβ+1β も同型射になる.
なお,上記の命題で fαβ+1 が同型射になることは,以下の命題から分かる.
- 命題.
ある射 a:A→B が a;b1:A→A=id を満たす b1:B→A と,b2;a:B→B=id を満たす b2:B→A を持つ時,a は同型射
証明:
b1;a=id;b1;a=b2;a;b1;a=b2;id;a=b2;a=id より,b1 は a の逆射より.
停止する initial sequence からは,initial algebra を構成できる.
- 補題. (initial algebra の構成)
α で initial sequence が停止する時,Fα0fα+1α−1F(Fα0) は initial algebra
証明:
任意の algebra FXaX について,任意の β≤α で hβ:Fβ0→X を以下のように定義する.
- β=0 の時
- h0:0→X は initial object の一意射で定める.
- β が極限順序数の時
- (hγ)γ<β は cocone になるため,一意射 hβ:Fβ0→X が存在する.これで定める.
- β=γ+1 と書ける時
- hβ=Fhγ;a で定める.
この時,fα+1α−1;hα=Fhα;a は容易に確かめられる.よって,hα:Fα0→X は準同型.また,準同型 k:Fα0→X について,任意の β≤α について kβ=fαβ;k とおくと,kβ=hβ となることは以下のように帰納法で示せる.
- β=0 の時
- initial object の一意性より正しい.
- β が極限順序数の時
- (hγ)γ<β=(kγ)γ<β であるため,kβ:Fβ0→X はその cocone への分解射になる.よって,colimit Fβ0 の一意性より正しい.
- β=γ+1 と書ける時
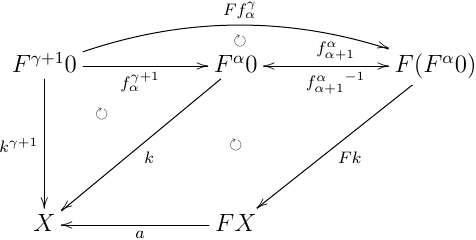
より,i.h. から kβ=F(fαγ;k);a=Fhγ;a=hβ より正しい.
よって,k=kα=hα より準同型は一意に定まることから,題意は示された.
双対的に,停止する terminal sequence から terminal coalgebra が構成できる.この具体的な設定としては,例えば F が colimit を保存すれば良い.
- 定理. (Adámek's Theorem)
F:C→C が colimit を保存する時,同型射 F(Fω0)∼Fω0 が存在し,initial algebra
証明:
Fω0∼colimn<ωFn+10∼F(Fω0) より.
なお,今回は ordinal chain で initial sequence を作っているが,上記の定理は countable chain complete ぐらいで成り立つ.双対的に terminal coalgebra も,F:C→C が limit を保存する時構成できる.さて,ここからが本題.
まず, algebra から coalgebra への準同型射を以下のように定義する.
- 定義. (relational F-morphism)
F-algebra FAaA 及び F-coalgebra BbFB について,以下の図式を満たす m:A→B を relational F-morphism と呼ぶ:
自明な relational morphism として以下のものが考えられる.
- 定義. fixed object
- 圏 C の自己関手 F:C→C を考える.対象 A∈∣C∣ が, A∼FA を持つ時, A を F における fixed object と呼ぶ.
- 系.
- initial algebra 及び terminal coalgebra は fixed object
- 系.
- fixed object A において, id:A→A は algebra FA∼A から coalgebra A∼FA への relational morphism
また, initial algebra から terminal coalgebra への relational morphism は一意になる.
- 命題.
initial F-algebra から terminal F-coalgebra への relational morphism は存在して一意.
証明:
terminal F-coalgebra B∼FB について, FB∼B は algebra より, initial algebra からの準同型射が存在し,これは B∼FB への relational morphism にもなる.また, initial algebra からの relational morphism を持ってくると,それは FB∼B への準同型射でもあるので,準同型射の一意性から一意になる.
さて, initial algebra と terminal coalgebra が一致するというのは,つまりその構成 object が同型になるということだが,この時 relational morphism としてその同型射を持ってくることができる.よって,上の relational morphism の一意性から, initial algebra と terminal coalgebra の一致を以下のように言い換えできる.
- 定義. (canonical isomorphic)
- initial algebra から terminal coalgebra の relational morphism が同型射の時, initial algebra と terminal algebra は canonical isomorphic であるといい,その時の relational morphism を canonical isomorphism と呼ぶ.
ところで,initial sequence と terminal sequence の間には relational morphism を設定できる.
- 定義. (relational morphism from initial sequence to terminal sequence)
hαα:Fα0→Fα1 を以下のように定義する:
- α=0 の時
- h00:0→1 は initial object から terminal object への一意射で定める.
- α が極限順序数の時
- まず,β<α を固定したとき,後述する hγβ:Fβ0→Fγ1 のようなものが考えられ,この時 (hγβ)γ<α は cone になり limit Fα1 への普遍射 hαβ:Fβ0→Fα1 が作れる.さらに,(hαβ)β<α は cocone になり colimit Fα0 からの普遍射 hαα:Fα0→Fα1 が作れる.なお,これは作る順序を変えても普遍性より同じ射が作れる.これで定める.
- α=γ+1 と書ける時
- hαα=Fhγγ で定める.
なおこの時, hβα:Fα0→Fβ1 を以下のように定義する.
hβα=⎩⎨⎧fβα;hββhααhαα;gβα(α<β)(α=β)(α>β)
ところで,全ての relational morphism は,initial sequence から terminal sequence への relational morphism に分解できる.
- 命題.
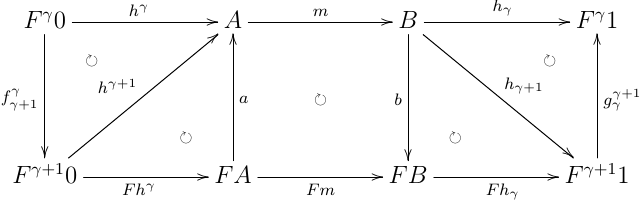
algebra FAaA,coalgebra BbFB について,relational morphism m:A→B が存在する時,initial algebra の構成の補題と同様の作り方で hα:Fα0→A を作成し,双対的に hα:B→Fα1 を作成した時,hαα=hα;m;hα
証明:
α に関する帰納法で示す.
- α=0 の時
- initial object の一意性から正しい.
- α が極限順序数の時
- hαα の定義と limit,colimit の一意性,i.h. から正しい.
- α=γ+1 と書ける時
以下が可換になるので,i.h. から hαα=Fhγγ=Fhγ;Fm;Fhγ=hα;m;hα より正しい.
ここまでが準備.
Algebraically Compact
initial algebra と terminal coalgebra が一致するような functor を, algebraically compact と呼ぶ.
- 定義. (algebraically compact functor)
- 圏 C に対して,自己関手 F:C→C が initial F-algebra と terminal F-algebra を持ち,canonical isomorphic になる時,F は algebraically compact だと呼ぶ.また,F が fixed object を持つならば algebraically compact である時,条件付き algebraically compact であると呼ぶ.
ところで, initial algebra や terminal coalgebra は fixed object なので, fixed object がないというのはつまり,関手が initial algebra や terminal coalgebra をそもそも作れる構造を持っていないということになる.つまり,条件付き algebraically compact とは,関手がそもそも initial algebra や terminal coalgebra を持てる構造にある前提で,その一致性があるというものになる.前の系を思い出すと, fixed object があれば relational morphism は作れるので,後重要なのは initial sequence の colimit と terminal sequence の limit が一致するかということになる.なお,自明だが algebraically compact なら条件付き algebraically compact である.
ついでに, category に対してのざっくりとした algebraically compact 性も定められている.
- 定義. (algebraically compact category)
- 圏 C に対して,任意の自己関手 F:C→C が algebraically compact である時, C を algebraically compact と呼ぶ.また,任意の fixed object を持つ F:C→C が algebraically compact である時,C を条件付き algebraically compact であると呼ぶ.
- 定義. (algebraically complete category)
- 圏 C に対して,任意の自己関手 F:C→C が initial F-algebra を持つ時,C を algebraically complete と呼ぶ.
algebraically complete というのは Fleyd が導入した言葉 .なお,algebraically compact category は algebraically complete category.さて,具体的にどういう条件下だと algebraically compact になるんだろうか? 1つの条件としては,以下のものがある.
- 定理. (algebraically compact の十分条件)
F:C→C について,以下を満たす時 F は algebraically compact
- ある α0 が存在して,任意の α>α0 で hαα:Fα0→Fα1 が同型射
- ある algebra FAaA 及び coalgebra BbFB の間の relational morphism AmB が存在する
証明:
この時,任意の α>α0 で hα;m;hα=hαα が同型射になる.ここで,eα=AmBhαFα1hαα−1Fα0hαA を考えると,
eα;eα=m;hα;hαα−1;hα;m;hα;hαα−1;hα=m;hα;hαα−1;hαα;hαα−1;hα=m;hα;id;hαα−1;hα=eα
を満たす.ところで,α0<α となる α 全体は集合を超えることが知られているので,α0<α における eα 全体が集合になるためには,ある α0<α1<α2 で eα1=eα2 となる必要がある .この時,
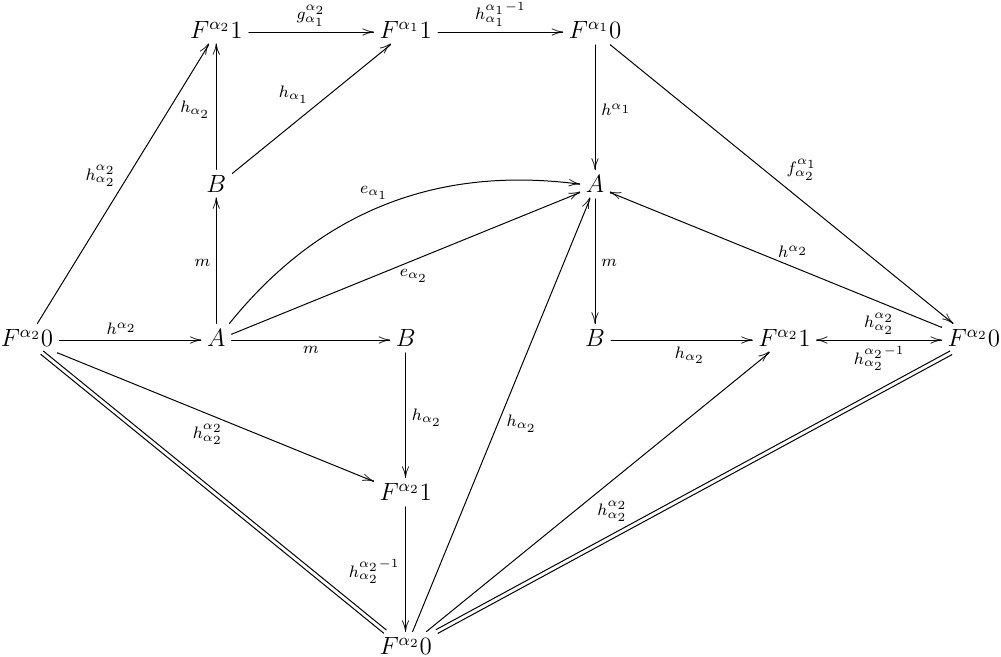
が可換になるので,(hα2α2;gα1α2;hα1α1−1);fα2α1=id で,逆も fα2α1;(hα2α2;gα1α2;hα1α1−1)=id が成り立つことが同様に確かめられる.よって,fα2α1 は同型射であり,この時 fα1+1α1 も同型射.つまり, initial sequence が停止し,Fα10fα1+1α1−1F(Fα10) は initial algebra になる.同様に Fα11gα1α1+1−1F(Fα11) は terminal coalgebra であり,hα1α1 は canonical iso になる.
ところで,ここから条件付き algebraically compact の条件が以下のようになることも分かる.
- 系. (条件付き algebraically compact の十分条件)
F:C→C について,以下を満たす時 F は algebraically compact
- ある α0 が存在して,任意の α>α0 で hαα:Fα0→Fα1 が同型射
証明:
fixed object の relational morphism が取れるため.
つまり,ある functor が fixed object を持つ,つまり initial algebra や terminal coalgebra を持てる構造になっていた時, initial sequence から terminal sequence の対応が同型射に落とし込める状況であればいいということになる.
具体例
では, initial algebra から terminal coalgebra への対応が同型になる状況は具体的にどういう状況なのかを見ていく.
- 補題.
CPO enriched な圏 C ,自己関手 C (CPO enriched とは限らない) において,以下を満たす (Fn1ln+1nFn+10)n∈N が存在するとする:
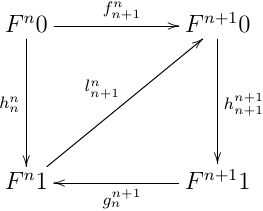
- 任意の n∈N で, hnn;ln+1n=fn+1n
- 任意の n∈N で, gnn+1;ln+1n;hn+1n+1⊑id
- 任意の n∈N で, ln+1n;hn+1n+1;gnn+1=id
この時, Fω0∼Fω1
証明:
Fω0 が terminal sequence の limit であることを示せば, limit の一意性から言える.まず,cone (hn:X→Fn1)n∈N を取ってきたとき,この cone から (hωω;gnω:Fω0→Fn1)n∈N への普遍射が hω=⨆m∈Nhm;lm+1m;fωm+1 であることを示す.
さて,任意の n∈N に対して hω=⨆m>nhm;lm+1m;fωm+1 ,つまり (hm;lm+1m;fωm+1)m∈N が単調増加であることを示す.
hm;lm+1m;fωm+1=hm+1;gmm+1;lm+1m;fm+2m+1;fωm+2=hm+1;gmm+1;lm+1m;hm+1m+1;lm+2m+1;fωm+2⊑hm+1;id;lm+2m+1;fωm+2=hm+1;lm+2m+1;fωm+2
ここから可換性を以下のように示せる:
hω;hωω;gnω=(⨆m∈Nhm;lm+1m;fωm+1);hωω;gnω=⨆m>nhm;lm+1m;fωm+1;hωω;gnω=⨆m>nhm;lm+1m;hωm+1;gnω=⨆m>nhm;lm+1m;hm+1m+1;gnm+1=⨆m>nhm;lm+1m;hm+1m+1;gmm+1;gnm=⨆m>nhm;id;gnm=⨆m>nhn=hn
さて,分解射 hω′:X→Fω0 を持ってきた時,
hω=⨆m∈Nhm;lm+1m;fωm+1=⨆m∈Nhω′;hωω;gmω;lm+1m;fωm+1=⨆m∈Nhω′;hωω;gmω;lm+1m;fωm+1=hω′;(⨆mhωω;gmω;lm+1m;fωm+1)
となる.ここで,
fωn;(⨆m∈Nhωω;gmω;lm+1m;fωm+1)=⨆m>nfmn;hmm;lm+1m;fωm+1=⨆m>nfmn;fm+1m;fωm+1=⨆m>nfωn=fωn
より, colimit の普遍射の一意性から ⨆m∈Nhωω;gmω;lm+1m;fωm+1=id .よって, hω′=hω より普遍射の一意性が示せる.
- 命題.
CPO enriched な圏 C , order enriched な関手 F:C→C について, T1g011lF0h11F1⊑id を満たす l:1→F0 が与えられた時, Fω0∼Fω1
証明:
ln+1n=Fnl とした時,それが上の補題の条件を満たすことを,数学的帰納法で確認する.
- 定理.
CPO enriched な圏 C , order enriched な関手 F:C→C について, T1g011lF0h11F1⊑id を満たす l:1→F0 が与えられる時, F は条件付き algebraically compact .
証明:
上の命題から Fω0∼Fω1 より.
つまり, CPO enriched な状況で, terminal sequence から initial sequence への対応を, id すれすれにいい感じに作れれば良いという感じ.ところで,この対応は pointed CPO の場合 bottom を持ってくることで作れる.
- 定理.
pointed CPO enriched な圏 C,order enriched な関手 F:C→C について,F は条件付き algebraically compact .
証明:
l:1→F0=⊥ で持ってきた時, T1g011lF0h11F1=⊥⊑id より.
さて,今圏は initial / terminal object を持ち, chain cocomplete / cochain complete としているが,空でない pointed CPO enriched な圏においては, chain cocomplete であれば null object (initial でも terminal でもある object) の存在を示せる.
- 命題.
空でない pointed CPO enriched な圏 C において,chain cocomplete なら null object が存在する.
証明:
空でないため圏から object A∈∣C∣ を適当に一つ持ってこれる.この時,以下の chain が作れる:
A⊥A⊥⋯
この colimit A∞ を考える.この構成射は AuA∞=A⊥Au′A∞=A⊥A∞ より,⊥:A→A∞ になる.任意の X∈∣C∣ について, A⊥X は cocone になる.この時,colimit からの普遍射 !:A∞→X が存在する.また, !′:A∞→X が存在した時, A⊥A∞!′X=A⊥X より分解射になる.この時,colimit の普遍性より !=!′ である.よって, A∞ は initial object になる.
また, X!A∞ があった時, X!A∞=X!A∞id=⊥A∞=X⊥A∞ より,任意の X∈∣C∣ について !:X→A∞ も一意に存在する.よって, A∞ は terminal object にもなる.
よって,空でない pointed CPO enriched な圏であれば, chain cocomplete を仮定するだけで良い.ところで,ここまでは条件付き algebraically compact ,つまり fixed object を持つ関手のみを対象にしてきたが,関手が CPO enriched ,つまり sup も保存するならば algebraically compact であることが言える.
- 定理.
pointed CPO enriched な圏 C,CPO enriched な関手 F:C→C について,F は algebraically compact .
証明:
l:1→F0=⊥ で持ってきた時,Fω0∼Fω1.ところで,実はこの時 Fω0∼F(Fω0) が示せる.これが成り立てば,Fω0 は fixed object になるので,題意が言える.よって,これを示す.これは,F(Fω0) が
0f10F0f21⋯Fn0fn+1n⋯
の colimit であることを示せれば,colimit の一意性から言える.
構成射を
fω′n:Fn0→F(Fω0)={0!F(Fω0)Ffωm(n=0)(n=m+1)
で作る.cocone (hn:Fn0→X)n∈N に対して,hω=⨆m∈NFhωω;Fgmω;lm+2m+1;hm+2 が普遍射になることを示す.
n=0 の時, initial object の普遍性より fω′0;hω=h0 になることは良い.n>0 の時,
fω′n;hω=Ffωn−1;(⨆m∈NFhωω;Fgmω;lm+2m+1;hm+2)=⨆m∈NFfωn−1;Fhωω;Fgmω;lm+2m+1;hm+2=⨆m>nFfmn−1;Fhmm;Flm+1m;hm+2=⨆m>nF(fmn−1;hmm;lm+1m);hm+2=⨆m>nFfm+1n−1;hm+2=⨆m>nfm+2n;hm+2=⨆m>nhn=hn
より,可換になることが示せる.また,分解射 hω′:F(Fω0)→X について,
hω=⨆m∈NFhωω;Fgmω;lm+2m+1;hm+2=⨆m∈NFhωω;Fgmω;lm+2m+1;fω′m+2;hω′=(⨆m∈NFhωω;Fgmω;Flm+1m;Ffωm+1);hω′=⨆m∈NF(hωω;gmω;lm+1m;fωm+1);hω′=F(⨆m∈Nhωω;gmω;lm+1m;fωm+1);hω′=Fid;hω′=hω′(∵colimit の普遍性より)
よって,分解射は一意になる.
なお,例えば pointed CPO による圏自体は,pointed CPO enriched であり,chain cocomplete なので今回の圏の条件を満たしている.よって,これ上の関手が fixed object を持って continuous function の順序を保存するか,continuous function space の sup を保存すれば,algebraically compact になる.
まとめ
とりあえず,関手が algebraically compact,つまり initial algebra と terminal algebra が iso になるには,
- どこかの α で Fα0∼Fα1 になること
- なんらかの algebra と coalgebra の間に relational morphism が作れること
が重要で,relational morphism の方は fixed object があれば作れるので,重要なのは initial sequence と terminal sequence がどこかで iso になるかということになる.
さらに, pointed CPO enriched な場合は,関手が order を保存すれば ⊥ からいい感じに Fω0∼Fω1 に繋げるような terminal sequence から initial sequence への射の列が作れる.なので, order を保存するぐらいで algebraically compact になる.
なるほどなという感じ (こなみ).







