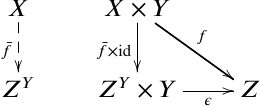ハイティング代数の性質

ハイティング代数の定義

まずは基本的なところから。最初に poset を導入する。

定義. 半順序 (partial order, poset)

集合 $A$ とそれ上の二項関係 $(\sqsubseteq) \subseteq A \times A$ の組 $(A, \sqsubseteq)$ で以下を満たすものを、半順序と呼ぶ:

反射律 (reflexivity)

任意の $x \in A$ について、$x \sqsubseteq x$

推移律 (transitivity)

任意の $x, y, z \in A$ について、$x \sqsubseteq y$ かつ $y \sqsubseteq z$ ならば、$x \sqsubseteq z$

反対称律 (anti-symmetric)

任意の $x, y \in A$ について、$x \sqsubseteq y$ かつ $y \sqsubseteq x$ ならば、$x = y$

束の定義方法は色々あるが、今回は poset ベースの束の定義を導入する。

定義. 束 (lattice)

半順序 $(A, \sqsubseteq)$ で以下を満たすものを、束と呼ぶ:

• 任意の $x, y \in A$ について、上限 $x \lor y \in A$ が存在する。この時、$x \lor y$ を結び (join) と呼ぶ
• 任意の $x, y \in A$ について、下限 $x \land y \in A$ が存在する。この時、$x \land y$ を交わり (meet) と呼ぶ

束は、幾つかの代数的性質が成り立つ。

定理. 束の性質

束 $(L, \sqsubseteq)$ について、以下が成り立つ:

交換律 (commutative)

任意の $x, y \in L$ について、$x \land y = y \land x$、$x \lor y = y \lor x$

結合律 (associative)

任意の $x, y, z \in L$ について、$x \land (y \land z) = (x \land y) \land z$、$x \lor (y \lor z) = (x \lor y) \lor z$

吸収律 (absorption)

任意の $x, y \in L$ について、$x \land (x \lor y) = x \lor (x \land y) = x$

冪等律 (idempotent)

任意の $x \in L$ について、$x \land x = x \lor x = x$

証明:

交換律，結合律，冪等律はいいと思うので，吸収律だけ示しておく．といっても，こいつもほぼ自明で，$x \leq x \lor y$，$x \land y \leq x$ より，下限，上限の定義から $x \land (x \lor y) = x$，$x \lor (x \land y) = x$．

束の中で、空集合に対する上限、下限が存在するもの、つまり最大元、最小元が存在するものを有界束と呼ぶ。

定義. 有界束 (bounded lattice)

束 $(L, \sqsubseteq)$ で以下を満たすものを，有界束と呼ぶ:

• ある $\top \in L$ が存在し、任意の $x \in L$ について $x \leq \top$ を満たす
• ある $\bot \in L$ が存在し、任意の $x \in L$ について $\bot \leq x$ を満たす

ハイティング代数は、有界束の中で冪対象を持つものである。

定義. ハイティング代数 (heyting algebra)

有界束 $(L, \sqsubseteq)$ で以下を満たすものを、ハイティング代数と呼ぶ:

• 任意の $x, y \in L$ について、$\{z \in L \mid x \land z \leq y\}$ の上限 $x \to y \in L$ が存在する。この時、$x \to y$ を冪 (exponential) または相対擬補元 (relative pseudo-complement) と呼ぶ

証明は省略するが，冪の例は $x \to x = \top$，$\top \to x = x$，$\bot \to x = \top$ などがある．

ハイティング代数の性質

分配律を満たす束を分配束という．

定義. 分配束 (distributive lattice)

束 $(L, \sqsubseteq)$ について、以下を満たすものを分配束と呼ぶ:

• 任意の $x, y, z \in L$ について、$x \land (y \lor z) = (x \land y) \lor (x \land z)$
• 任意の $x, y, z \in L$ について、$x \lor (y \land z) = (x \lor y) \land (x \lor z)$

なお，片方のみ成り立てば分配束になる．

定理. 分配束の条件

束 $(L, \sqsubseteq)$ について、以下は同値．

1. $(L, \sqsubseteq)$ は分配束
2. 任意の $x, y, z \in L$ について、$x \land (y \lor z) = (x \land y) \lor (x \land z)$
3. 任意の $x, y, z \in L$ について、$x \lor (y \land z) = (x \lor y) \land (x \lor z)$

証明:

1 ならば 2，1 ならば 3 は自明．2 ならば 1 は，

$$(x \lor y) \land (x \lor z) = ((x \lor y) \land x) \lor ((x \lor y) \land z) = x \lor (x \land z) \lor (y \land z) = x \lor (y \land z)$$

より，示せる．3 ならば 1 も対称的に証明できる．

ハイティング代数は、分配束になる．

定理. ハイティング代数の分配律

ハイティング代数は，分配束である．

証明:

• $x \land y \leq x \land (y \lor z)$
• $x \land z \leq x \land (y \lor z)$

より，$x \land (y \lor z)$ は $x \land y$，$x \land z$ の上界になる．よって，$(x \land y) \lor (x \land z) \leq x \land (y \lor z)$．また，

• $x \land y \leq (x \land y) \lor (x \land z)$
• $x \land z \leq (x \land y) \lor (x \land z)$

より，

• $y \leq (x \to (x \land y) \lor (x \land z))$
• $z \leq (x \to (x \land y) \lor (x \land z))$

よって，$x \to (x \land y) \lor (x \land z)$ は $y$，$z$ の上界より $y \lor z \leq (x \to (x \land y) \lor (x \land z))$．ここから，

$$x \land (y \lor z) \leq x \land (x \to (x \land y) \lor (x \land z)) \leq (x \land y) \lor (x \land z)$$

よって，$x \land (y \lor z) = (x \land y) \lor (x \land z)$ より，分配束になる．

ついでにだが、通常の有界束は分配律が成り立つとは限らない。反例は以下のもの:

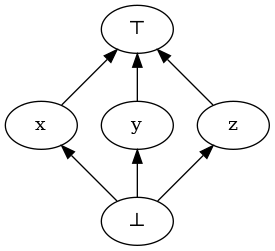
この時、$x \lor (y \land z) = x \neq \top = (x \lor y) \land (x \lor z)$ になる。さて，束の元には補元が存在する場合がある．

定義. 補 (complement)

有界束 $(L, \sqsubseteq)$ の元 $x \in L$ について，

• $x \land y \leq \bot$
• $\top \leq x \lor y$

を満たす $y \in L$ を $x$ の補と呼ぶ

$\top$ と $\bot$ は互いに補の関係になる．なお，有界束において一般に補は一意とは限らない．例えば，上の分配律が成り立たない束において，$x$ の補は $y$，$z$ 両方になる．もちろん存在するとも限らない．これは，線形な束を思い描いてみるといいだろう．ところで，分配束において補は存在するなら一意に定まる．

定理. 分配束における補の一意性

有界な分配束 $(L, \sqsubseteq)$ について，

• 任意の $x, y, z \in L$ について、$x \land (y \lor z) = (x \land y) \lor (x \land z)$
• 任意の $x, y, z \in L$ について、$x \lor (y \land z) = (x \lor y) \land (x \lor z)$

が成り立つ時，任意の $x \in L$ についてその補は高々1つである

証明:

$x \in L$ の補 $y_1 \in L$，$y_2 \in L$ が存在する時，

$$y_1 = y_1 \land (y_2 \lor x) = (y_1 \land y_2) \lor (y_1 \land x) = (y_1 \land y_2) \lor (y_2 \land x) = y_2 \land (y_1 \lor x) = y_2$$

より，$y_1 = y_2$．よって，存在すれば補は一意．

ハイティング代数において補は存在するとは限らないが，ハイティング代数は分配束より存在すれば一意である．さらに，ハイティング代数においては補が存在すればその形を特定できる．

定義. 擬似補 (pseudo-complement)

ハイティング代数 $(H, \sqsubseteq)$ について、その要素 $x \in H$ に対し、$x \to \bot$ を擬似補と言い、$\neg x$ と表記する

ハイティング代数において，補が存在すればそれは $\neg x$ と一致する．

定理. 擬似補と補の一意性

ハイティング代数 $(H, \sqsubseteq)$ の元 $x \in H$ について，その補が存在する時，それは $\neg x$ のみである

証明:

$x \in H$ の補 $y \in H$ が存在する時，$x \land y \leq \bot$ より $y \leq \neg x$ である．この時，

• $x \land \neg x \leq \bot$
• $\top \leq x \lor y \leq x \lor \neg x$

より，$\neg x$ は補である．さらに，ハイティング代数は分配束なので，補は $\neg x$ のみである．

ハイティング代数ではド・モルガン則は片方のみ成り立つ．

定理. ド・モルガン則 (De Morgan's law)

ハイティング代数 $(H, \sqsubseteq)$ について、以下が成り立つ:

• 任意の $x, y \in H$ について、$\neg x \land \neg y = \neg (x \lor y)$

証明:

$$(x \lor y) \land \neg x \land \neg y = (x \land \neg x \land \neg y) \lor (y \land \neg \land \neg y) = \bot \lor \bot \leq \bot$$

より，$\neg x \land \neg y \leq \neg (x \lor y)$．また，

$$x \land \neg (x \lor y) \leq (x \land \neg (x \lor y)) \lor (y \land \neg (x \lor y)) = (x \lor y) \land \neg (x \lor y) \leq \bot$$

より，$\neg (x \lor y) \leq \neg x$．対称性より $\neg (x \lor y) \leq \neg y$．よって，$\neg (x \lor y) \leq \neg x \land \neg y$ より，$\neg x \land \neg y = \neg (x \lor y)$．

ブール代数と二重否定変換

ハイティング代数のインスタンスにブール代数がある．

定義. ブール代数 (boolean algebra)

分配束 $(L, \sqsubseteq)$ で以下を満たすものを、ブール代数と呼ぶ:

• 任意の $x \in L$ について、その補が存在する

定理. ブール代数はハイティング代数

ブール代数 $(B, \sqsubseteq)$ は，ハイティング代数である

証明:

$x, y \in B$ について，$x$ の補を $a$ とする．この時，$x \to y = a \lor y$ を示す．

$$x \land (a \lor y) = (x \land a) \lor (x \land y) = x \land y \leq y$$

であり，$x \land z \leq y$ となる $z \in B$ について，

$$z = z \land (a \lor x) = (z \land a) \lor (x \land z) \leq a \lor y$$

より，$a \lor y$ は $x \to y$ の条件を満たす．よって，任意の元について冪が存在するため，$(B, \sqsubseteq)$ はハイティング代数．

ハイティング代数がブール代数になる条件として，以下が知られている．

定理. ブール代数の同値条件

ハイティング代数 $(H, \sqsubseteq)$ について，以下は同値

1. $H$ はブール代数
2. 任意の $x \in H$ について，$x \lor \neg x = \top$
3. 任意の $x \in H$ について，$\neg \neg x = x$

証明:

$x \in H$ について $x \land \neg x \leq \bot$ であること，ブール代数がハイティング代数であることから，1 と 2 の同値性はいいと思う．

2 から 3 は，

$$\neg \neg x = \neg \neg x \land (x \lor \neg x) = (\neg \neg x \land x) \lor (\neg \neg x \land \neg x) = \neg \neg x \land x$$

$$= (\neg \neg x \land x) \lor (x \land \neg x) = (\neg \neg x \lor \neg x) \land x = x$$

より示せる．3 から 2 は，ハイティング代数で適用できるド・モルガン則を使用して，

$$x \lor \neg x = \neg \neg (x \lor \neg x) = \neg (\neg x \land \neg \neg x) = \neg \bot = \top$$

より示せる．

ブール代数では，2つめのド・モルガン則も示せる．

定理. ド・モルガン則 (De Morgan's law)

ブール代数 $(B, \sqsubseteq)$ について、以下が成り立つ:

• 任意の $x, y \in H$ について、$\neg x \lor \neg y = \neg (x \land y)$

証明:

ブール代数では二重否定の除去ができることから，ハイティング代数上で成り立つド・モルガン則を使用して，

$$\neg x \lor \neg y = \neg \neg (\neg x \lor \neg y) = \neg (\neg \neg x \land \neg \neg y) = \neg (x \land y)$$

のように示せる．

さて，ハイティング代数からブール代数への変換方法として，二重否定変換というものが知られている．これは，名前の通り全ての元に二重否定をかますような変換だ．それを示すため，まず準備として補題を用意する．

補題.

ハイティング代数 $(H, \sqsubseteq)$ について，以下が成り立つ:

• 任意の $x \in H$ について，$x \leq \neg \neg x$
• 任意の $x, y \in H$ について，$x \leq y$ ならば $\neg y \leq \neg x$

証明:

$\neg x \land x \leq \bot$ より，$x \leq \neg \neg x$．また，$x \leq y$ の時，

$$x \land \neg y \leq y \land \neg y \leq \bot$$

より，$\neg y \leq \neg x$．

補題.

ハイティング代数 $(H, \sqsubseteq)$ について，以下が成り立つ:

• 任意の $x \in H$ について，$\neg \neg \neg x = \neg x$
• 任意の $x, y \in H$ について，$\neg \neg (x \land y) = \neg \neg x \land \neg \neg y$

証明:

前の補題から，$\neg x \leq \neg \neg \neg x$．また，$\neg x \leq \neg \neg x$ から $\neg \neg \neg x \leq \neg x$．よって，$\neg \neg \neg x = \neg x$．

また，$x \land y \leq x$，$x \land y \leq y$ から，$\neg \neg (x \land y) \leq \neg \neg x$，$\neg \neg (x \land y) \leq \neg \neg y$ より，$\neg \neg (x \land y) \leq \neg \neg x \land \neg \neg y$．さて，後 $\neg \neg x \land \neg \neg y \leq \neg \neg (x \land y)$ を示せれば良い．これを示すには，$\neg (x \land y) \land \neg \neg x \land \neg \neg y \leq \bot$ を示せれば良い．

ところで，$\neg (x \land y) \land x \land y \leq \bot$ より，

$$\neg (x \land y) \land x \leq \neg y = \neg \neg \neg y$$

であるため，$\neg (x \land y) \land x \land \neg \neg y \leq \bot$ である．同様に $x$ についても同じ操作から，$\neg (x \land y) \land \neg \neg x \land \neg \neg y \leq \bot$ となる．よって，$\neg \neg (x \land y) = \neg \neg x \land \neg \neg y$．

これより，二重否定変換はハイティング代数上の準同型になり，二重否定の除去を付加できる．これにより，ハイティング代数からブール代数を生成できる．

定理. 二重否定変換 (double-negation translation)

ハイティング代数 $(H, \sqsubseteq)$ について，$H_{\neg\neg} = (\{\neg \neg x \mid x \in H\}, \sqsubseteq)$ はブール代数である

証明:

前の補題から，元の $H$ の $\land$ は $H_{\neg\neg}$ でも閉じている．また，$x \leq \neg\neg x$ より，冪も保存される．よって，$H_{\neg\neg}$ はハイティング代数．さらに，$\neg\neg(\neg\neg x) = \neg\neg x$ であり，$H_{\neg\neg}$ はブール代数になる．

圏論的視点

今までは通常の束論の議論でハイティング代数を取り扱ってきたが，圏論的な議論もしておく．まず，半順序での最大下界，最小上界は，poset での直積，直和になる．これは，定義を比べてみれば分かると思う．そして，最小元，最大元は始対象，終対象に相当する．よって，有界束とは，finitely complete かつ cocomplete な poset のことになる [1] ．

定義. 有界束

poset $C$ が有界束とは，以下を満たすこと

• 有限積を持つ (finitely complete)
• 有限余積を持つ (finitely cocomplete)

ハイティング代数は，有界束のなかで CCC (Cartesian Closed Category) になるものである．すなわち，冪も持つような poset になる．

定義. ハイティング代数

有界束 $C$ がハイティング代数とは，以下を満たすこと

• CCC である

冪の定義も照らし合わせてみるとそのままだが，一応確認しておくと，

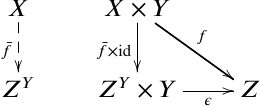
が冪対象の定義で，この時 $z^y \land y = z^y \times y \leq z$ かつ $x \times y = x \land y \leq z$ となる $x$ について $x \leq z^y$ となる．冪の随伴関係 $C(X \times Y, Z) \simeq C(X, Z^Y)$ がそのままで，つまりハイティング代数とは，$- \land Y$ が右随伴を持つような有界束のことになる．ついでに，CCC で finite coproduct を持つような圏を BCCC (BiCartesian Closed Category) と言うらしい．ハイティング代数は，この言葉を使うと poset で BCCC になるものと言える．

さて，左随伴の有用な性質として，余極限を保存すると言うものがある．つまり，ハイティング代数では $x \land -$ は余極限を保存する．ここから直ちに分配束であることが導ける．

定理.

ハイティング代数は，分配束である．

証明:

$x \land -$ は余極限を保存するため，

$$x \land \bigvee_y y = \bigvee_y x \land y$$

である．

ところで，$\neg$ はハイティング代数 $H$ 上の反変関手 $\neg: H \to H^{\mathrm{op}}$ になる．逆にも $\neg: H^{\mathop{op}} \to H$ を張れて，こいつらは随伴になる．一般に，$H$ の対象 $X$ について，$X^-: H \to H^{\mathrm{op}}$ は左随伴になる．

定理.

ハイティング代数 $H$，$X \in |H|$ について，$X^-: H \to H^{\mathrm{op}}$ は右随伴を持つ．

証明:

$$H^{\mathrm{op}}(X^Y, Z) \simeq H(Z, X^Y) \simeq H(Y \times Z, X) \simeq H(Y, X^Z)$$

より，$X^-: H^{\mathrm{op}} \to H$ が右随伴になり，$X^- \dashv X^-: H \to H^{\mathrm{op}}$ になる．

ところで，$\neg: H \to H^{\mathrm{op}}$ が左随伴を持つ場合がある．$\neg: H^{\mathrm{op}} \to H$ がその左随伴になる $H$ がブール代数である．

定義. ブール代数

ハイティング代数 $H$ がブール代数とは，以下を満たすこと:

• $\neg \dashv \neg: H^{\mathrm{op}} \to H$

この定義がブール代数の条件に合うことを確認する前に少々寄り道する．さて，随伴同値 (adjoint equivalence) と言う条件がある．これは，随伴による単子 (unit)，余単子 (counit) が自然同型になることである．

定義. 随伴同値

随伴 $F \dashv G$ について，その単子，余単子が自然同型である時，$F \dashv G$ を随伴同値という．

随伴同値の場合，$F \dashv G$ かつ $G \dashv F$ になる．

定理.

随伴 $F \dashv G$ が随伴同値ならば，$G \dashv F$ である

証明:

unit $\eta: 1 \Rightarrow G \circ F$，counit $\epsilon: F \circ G \Rightarrow 1$ が自然同型である時，それぞれの逆射 $\epsilon^{-1}: 1 \Rightarrow F \circ G$，$eta^{-1}: G \circ F \Rightarrow 1$ が存在する．この時，

• $G \xrightarrow{G \epsilon^{-1}} GFG \xrightarrow{\eta^{-1}_G} G$
• $F \xrightarrow{\epsilon^{-1}_F} FGF \xrightarrow{F \eta^{-1}} F$

はそれぞれ

• $F \xrightarrow{F \eta} FGF \xrightarrow{\epsilon_F} F$
• $G \xrightarrow{\eta_G} GFG \xrightarrow{G \epsilon} G$

の逆射になる．よって恒等射になるため，それぞれが unit / counit になる随伴 $G \dashv F$ が作れる．

ところで，$\neg \circ \neg$ は恒等関手，つまり二重否定の除去が成り立つとすると，この時 $\neg \dashv \neg: H \to H^{\mathrm{op}}$ の unit は自然同型になる．また，unit が自然同型になるならば二重否定の除去ができる．つまりブール代数とは，ハイティング代数で $\neg$ が随伴同値になるものである [2] ．

定理. ブール代数の条件

ハイティング代数 $H$ について，以下は同値

1. $H$ はブール代数
2. $\neg \circ \neg: H \to H$ は恒等関手
3. $\neg \dashv \neg: H \to H^{\mathrm{op}}$ は随伴同値

証明:

3 から 1 はよい．1 から 2 は，

• $H(Y, \neg X) \simeq H^{\mathrm{op}}(\neg X, Y) \simeq H(X, \neg Y)$
• $H(\neg X, Y) \simeq H^{\mathrm{op}}(X, \neg Y) \simeq H(\neg Y, X)$

より，$\neg X \xrightarrow{1} \neg X$ に対応する射

• $X \leq \neg\neg X$
• $\neg\neg X \leq X$

が存在する．よって，$\neg\neg X = X$ であることより，示せる．2 から 3 は，unit / counit が恒等関手から恒等関手への口頭変換になることから自明．

ところで，ブール代数に限らずハイティング代数では $\neg \dashv \neg$ だった．随伴からはモナドが作れるので，$\neg\neg$ はモナドになる．この時，$\neg\neg(\neg\neg x) \leq \neg\neg x$ がモナドの自然変換から作れるため，$\neg\neg$ により作られる subcategory がハイティング代数であれば，$\neg\neg(\neg\neg x) = \neg\neg x$ になる．つまり，$\neg\neg$ により作られる subcategory はブール代数になる．$\neg\neg$ により作られる subcategory がハイティング代数であることは，finite product / finite coproduct / implication を保存することを地道に証明する方法しか知らないので割愛する．誰か他の方法知ってたら教えて欲しい [4]．

まとめ

てことで，ハイティング代数は BCCC になる poset で，ブール代数は $0^-$ が随伴同値になるハイティング代数だよ，何か問題でも?

なお，$X^-$ が左随伴になるって話から，$(x \lor y) \Rightarrow z = (x \Rightarrow z) \land (y \Rightarrow z)$ が直ちに示せたり [3]，随伴 $\neg \dashv \neg$ の同値性 $H(Y, \neg X) \simeq H(X, \neg Y)$ に $X = \neg Z$，$Y = Z$ すれば $Z \leq \neg\neg Z$ が直ちに示せたりして便利．まあ，その証明が相手に通じるかは置いといて．てことで，今回は以上．

[1]	finitely complete になるには厳密には，finite product と equalizer の存在が必要になる．ただ，今回は poset なので，任意の対象間に射はたかだか一つしか存在しないため，equalizer は自明に存在する．finitely cocomplete も同様．

[2]	一般には，$F \dashv G$，$G \dashv F$ の時に $F \dashv G$ が随伴同値になるとは限らない．

[3]	$X^-$ は反変であることに注意．反変なので，product / coproduct が逆転する．

[4]	某勉強会でそのうち出てくる?