graded monad から monad への埋め込み

エフェクトシステムを monad で近似する

エフェクトシステムによって，静的型情報をより詳細にできるわけだが，実行機械を作る時にはこのエフェクト情報を特に使わない実行方法が得られる場合が多い．もし， graded monad による言語を monad による言語に近似できれば， graded monad 用の実行方法をわざわざ作らなくても， monad の実行方法を流用できる．

では，ある graded monad が与えられた時にそいつによる意味論をうまく近似するような monad が作れないだろうかというので，以下のようなことが考えられる．

monad への埋め込み

monoidal category $(E, \cdot, 1)$ において，終対象 $F \in |E|$ が存在するとする．

graded monad $(T: E \to [C, C], \eta: \mathrm{Id} \Rightarrow T 1, \mu: T - ; T - \Rightarrow T (- \cdot -)$ について， $(\hat{T}: C \to C, \hat{\eta}: \mathrm{Id} \Rightarrow \hat{T}, \hat{\mu}: \hat{T}^2 \Rightarrow T)$ を次のように与える．

• $\hat{T} = T F$
• $\hat{\eta}_A = A \xrightarrow{\eta_A} T 1 A \xrightarrow{T (1 \to F)} \hat{T} A$
• $\hat{\mu}_A = \hat{T}^2 A \xrightarrow{\mu_{F,F}} T (F \cdot F) A \xrightarrow{T (F \cdot F \to F)} \hat{T} A$

こいつは， monad になる．規則を満たすかは，次のように確認できる．

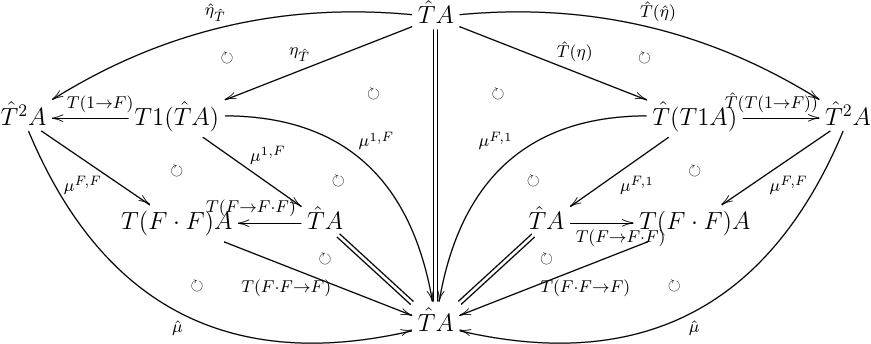
こちらは， $\hat{\eta}_{\hat{T}}; \hat{\mu} = \hat{T} \hat{\eta}; \hat{\mu} = \mathrm{id}$ を計算したやつ．

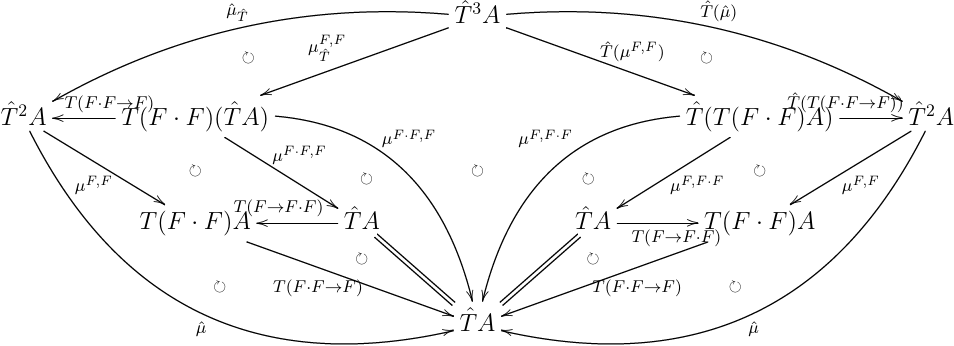
こちらは， $\hat{\mu}_{\hat{T}}; \hat{\mu} = \hat{T} \hat{\mu}; \hat{\mu}$ を計算したやつ．

なお， $\mu: T -; T - \Rightarrow T (- \cdot -): E \times E \to [C, C]$ は自然変換なので，以下を満たし，

$F$ は終対象なので， $F \xrightarrow{f} F \cdot F \xrightarrow{g} F = \mathrm{id}_F$ なことに注意．

そして，自然変換 $T(\epsilon \to F): T(\epsilon) \Rightarrow \hat{T}$ が存在する．

preordered monoid の終対象とは， preorder での最大元に当たる．なのでこの埋め込みは，エフェクトシステム的な直感にもマッチしていて，エフェクトシステムがエフェクトの見積もりを細かくして型に情報として載せるものだったわけだけど，その細かく見積もった情報を実行時に使わないで，最大のエフェクトで動作だけ近似するというわけだ．

埋め込みによる意味論の保存

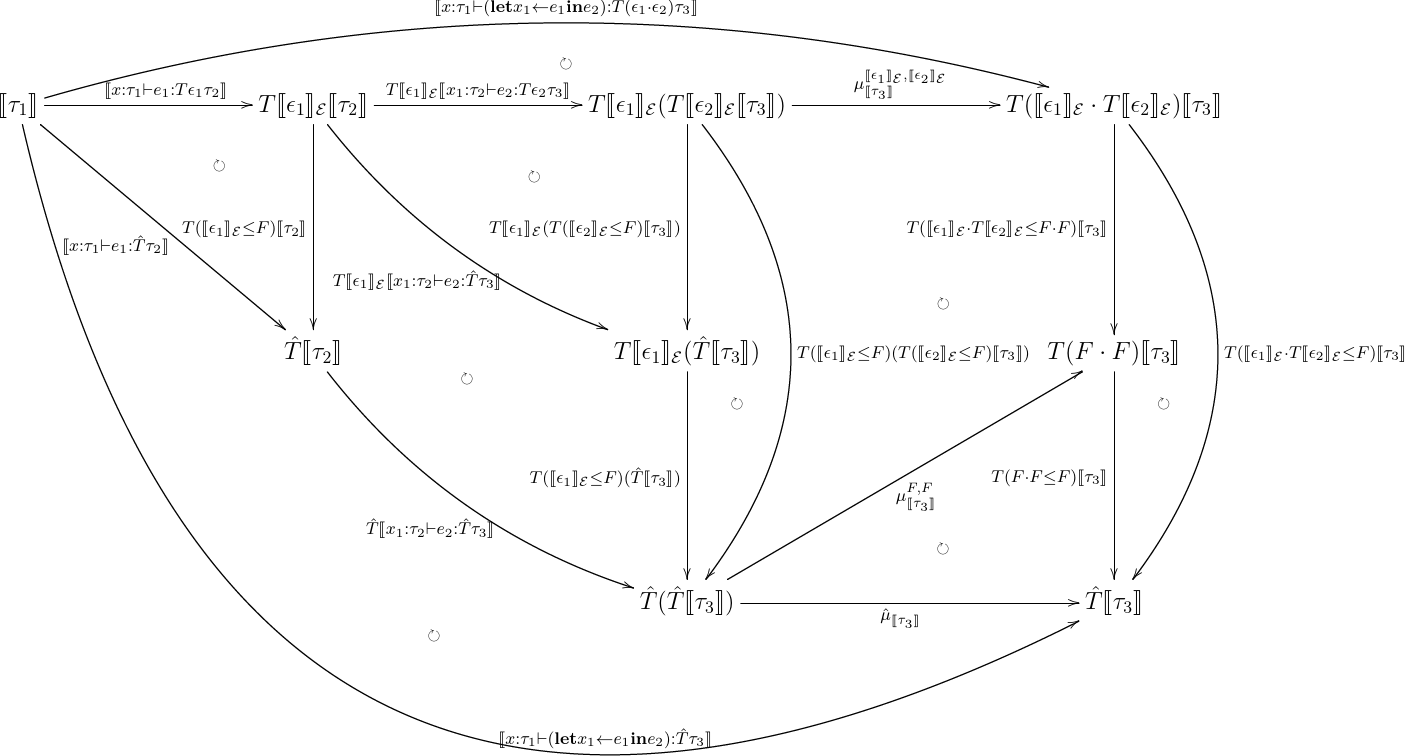
もちろんこの埋め込みが， graded monadic な意味論を monadic な意味論にうまく近似できなければ意味がない．なので，それを確かめてみる．近似できるとは，つまり以下のものが成り立つということだ．

左側が graded monadic な意味論，右側が monadic な意味論になる．ここで， $i: T ⟦e⟧_{\mathcal{E}} \Rightarrow \hat{T}$ は埋め込み $T(\epsilon \to F)$ になる． 以前の記事 で上げた構文要素それぞれで，帰納法を回してこれが一致することを示してみる．なお， effect を発生させる関数は graded monad での意味論と monad での意味論で解釈が異なる．なので，こいつらについては，

が成り立つという仮定を置く．この下で，以下のように帰納法を用いて示すことができる．

lift

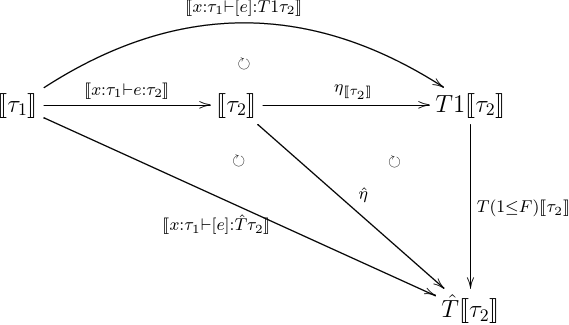
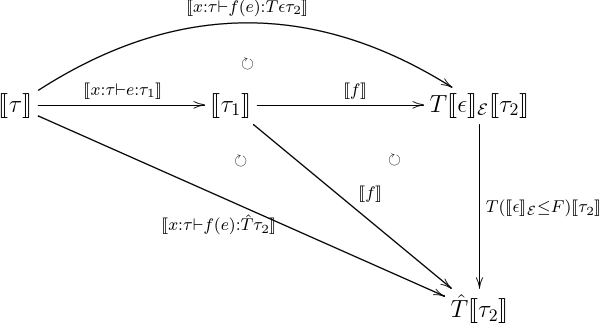
effectful app

let

cast

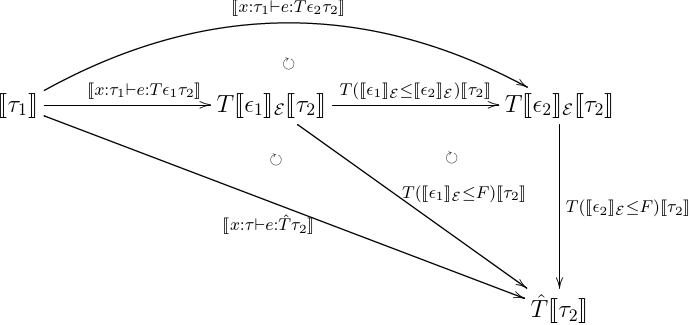
ちゃんと成り立ってるっぽい．

まとめ

この埋め込み以外にも graded monad からその近似としての monad を作る方法はありそう．一般的には， graded monad が与えられた時，いい感じの性質を満たす monad を持ってこれればそいつでいい感じに近似できるよみたいな研究があるっぽい．この手法は， graded monad をプログラミングツールとして使う場合も役に立ちそう．

こちらからは以上です．