文脈依存 PEG による Haskell パーサ
2022年02月23日に投稿 • カテゴリ:フレームワーク
前に PEG パーサジェネレータライブラリ ptera を作っているという話をしたが,今回はその第二弾.ptera で Haskell2010 の文法パーサを例に追加してみたんだが,その過程で色々あったのでその備忘録.
結論から言うと,ptera に前回から以下の拡張を加えた.
- 先読みを強化し,もうちょっとちゃんと機能するように
- 文脈依存でパースができるようにした
後は,Template Haskell で文法書けるようにしたりもしたが,まあそれはいいでしょ.
Haskell2010 と ptera
ptera でひとまず Template Haskell で文法が書けるフロントエンド部分作った後,Haskell 2010 ぐらいパースできないと使い物にならないなあと言う感じで Haskell の example project 書いてみたんだが,ここで色々つまづいてしまった.主に今回説明する ptera の拡張は,この example project 書くために入れたと言っても過言ではない.まあ,普通に Haskell 2010 パーサ実装以外でも役に立つ機能で,今後僕は普通に使っていく機能ではあると思うので足りない機能ではあったんだろうけど.
さて, Haskell 2010 の文法 自体はまあ大きくはあるんだが,曖昧さ含む部分が結構あるのを除けば割と普通の文脈自由文法によって定義されていると思う [1].ただ,Haskell 2010 のパーサを実装する上で凶悪なものとして知られているのが,レイアウトルールと呼ばれる規則だ.
レイアウトルールとはインデントによって文法の意味を変えるようなパース時のメタ規則だ [2].レイアウトルールは Haskell 内の用語で,一般的にはオフサイドルールなどと呼ばれることもある.仕様自体は一見そこまで複雑なものではなく,基本的にはトークナイズの後にそれぞれのトークンの位置を見て「 {」,「 ;」,「 }」を自動で挿入するようなものになっている.これを前段にかます前提で文脈自由文法は定義されていて,例えば
1 2 3 | f :: Int f = x where x = 1 |
みたいなプログラムは,
1 2 3 4 | {f :: Int ;f = x where {x = 1 }} |
のように明示的にレイアウトが判別できるようなプログラムに変換された後,パースが走るという感じだ.さて,この話を聞く限りはそこまで複雑な話であるように見えないだろう.実際,ここまでの話で終わるならレイアウト・ルールがここまでパーサ実装者にとって凶悪認定されることはないだろう.パーサ実装者の頭を悩ますのは,レイアウトルールの規則の中の1つ, Haskell 2010 Language Report 10.3 Layout に存在する以下の規則だ:
L (t : ts) (m : ms) = } : (L (t : ts) ms) if m ≠ 0 and parse-error(t) (Note 5)
Note 5. The side condition parse-error(t) is to be interpreted as follows: if the tokens generated so far by L together with the next token t represent an invalid prefix of the Haskell grammar, and the tokens generated so far by L followed by the token "}" represent a valid prefix of the Haskell grammar, then parse-error(t) is true.
Note 5. 右隅の条件 parse-error(t) は次のように解釈されます: L がこれまで生成したトークンと次のトークン t が,Haskell 文法の無効な接頭辞を成し,L がこれまで生成したトークンと "}" が Haskell 文法の有効な接頭辞を成す場合,parse-error(t) は真である.
L は文法に入る前の前処理で,トークンの位置を見ていい感じに「 {」,「 ;」,「 }」を挿入する前処理関数の実装になっている.この規則以外はトークンとその位置から決まるのだが,この規則だけはなんと文法のパースができるかに依存することになる.この関数を愚直に実装するなら,トークン列の全ての位置でパースしてみて失敗しないかを見ることになるだろう.さらに厄介なのが,パースが失敗した後に「 }」が挿入されトークン列が 変わる ということだ.そのため,今まで試してきたパースとトークンが挿入された後では結果が異なる可能性が十分あり,予測も難しいということになる.
我らが GHC も例に漏れずレイアウトルールの実装ではかなり苦労しており,時々パーサに関するイシューが上がっている [3].また,Haskell のパーサは GHC 以外でも Haskell コミュニティ内でさえいくつも実装が行われている.HSE (haskell-src-exts) と言うライブラリもその1つで Hoogle, stylish-haskell などで使われている.HSE ももちろんレイアウトルールには対応しているわけだが,その実装にもかなり根深い問題として,空の where をパースできないと言うことが知られている [4].
このような苦労をしてまでこのレイアウトルールを入れることに意味はあるのだろうか? このルールさえなければ,おそらく GHC や他の実装もトークナイザとパーサを完全に切り離して実装できるはずだ.このルールが役に立つ例として,例えば以下のケースがある:
1 2 3 4 | main = do pure x where x = 0 |
この場合,詳細は省くが
1 2 3 4 | {main = do {pure x ;}where {x = 0}} |
のような形でトークンが挿入されることになる.このうち, where の手前の } がパースエラーによって挿入されるものになる.このようなプログラムはしばしば書かれるので,割とパースエラーによるレイアウトに依存したプログラムはあるはずだ.後は,Haskell Language Report でも例として紹介されている以下のケースだ:
1 | let x = e; y = x in e' |
この場合は,
1 | let {x = e; y = x }in e' |
のようにトークンが挿入されることになる.流石にこういうプログラムを書く人は少ないかもしれないが, let x = 1 in x + 1 みたいなワンライナーを書く人は割といるんじゃないだろうか.このようなプログラムはパースエラーによるレイアウト終了のルールに頼っていることになる.割と便利ではあるのだ.正しく実装するのが非常に困難なだけで.
さて,具体的にこのレイアウトルールに則ったパースをどう行うかだが,GHC ではどうやっているかというと,GHC が使っている LALR パーサジェネレータに,error トークンというそのトークンの位置でパースが失敗した場合に復帰するようなうってつけの機能が実装されており,それを使用している.GHC の場合は,そもそもトークナイザとパーサが分かれてはいるものの深く連動しており,互いにコンテキストを共有しあっているという (恐ろしい) 実装になっていて [5],かなり改修が困難なものになっている.そのため,昔はコーナケースのパースイシューを提示されても修正が不可能みたいなこともあり (今も眠っているイシューがあるかもしれない),バージョンアップ毎のリファクタリングでかろうじて拾っていくみたいな状況になっている.
例に漏れず ptera でもレイアウトルールに対応するため大幅な機能アップデートを余儀なくされた.特に,パース途中で入力のトークン列が変わるというのは,PEG と大変相性が悪い.最終的にその部分については,それなりに満足いく対応はできたが,代わりに幾つかのものを捨てることにもなった.その対応方法について紹介すると言うのが,今回の内容だ.対応方針は「パースアクションで文脈を変更できるようにし,その際のメモ化は捨てる」だ.この結果,純粋な (アクションで文脈をいじらない) PEG が入力なら相変わらず線形時間でパース可能だが,全体としては ptera は線形時間パースを捨てるという道を選んだ.
文脈依存 PEG とレイアウトルール
さて,ptera で Haskell のパーサを実装するとなった段階でまず着手したことは,そもそもトークン列をパースの状態によって変えるのをやめられないかということだった.入力トークン列がパース途中に変わる場合かなり実装が手間だし,そもそも PEG とかなり相性が悪い.ただ,まあこんぐらいパースできないと後々困るので,方法をいくつか模索した.その結果,PEG ではちょっと難しそうだったので,文法を拡張する方向でいくことにした.ただ拡張の方向として,文法に何か規則を加えたわけでなく,文脈依存のアクションを許すようにした.具体的には,文脈を規則毎に更新したり,文脈によってパースを失敗させたりできる.
コンセプトとしては,
body ::= open body? close
open ::= "(" | "{" | "["
close ::= ")" | "}" | "]"
みたいな文法があった時に,
body ::= open body? close
open ::= "(" { l ↦ push("(",l) }
| "{" { l ↦ push("{",l) }
| "[" { l ↦ push("[",l) }
close ::= ")" { l ↦ pop(l) | !empty(l) & front(l) = "(" }
| "}" { l ↦ pop(l) | !empty(l) & front(l) = "{" }
| "]" { l ↦ pop(l) | !empty(l) & front(l) = "[" }
みたいな形で文脈の変更アクションと文脈検査を追加できるみたいな感じ.読み方としては,{} で囲まれた部分が文脈操作を現していて,x ↦ y で文脈 x を y に更新する. | で条件をつけることもでき,その場合条件が成立しなければその部分の選択を失敗させ,次の選択にいく.最初に例示した文脈なしの場合は開く数と閉じる数が一緒かどうかを検査しないので,例えば ([{])} みたいな対応がめちゃくちゃなものを accept してしまう.しかし文脈付きのやつはその対応を文脈上で検査することで,ちゃんと括弧の種類が対応しているものでないと accept しない.もちろんこの例は,次のように書けば文脈上での検査は不要になる:
body ::= "(" body? ")"
| "[" body? "]"
| "{" body? "}"
ただ,これぐらいの構文定義ならいいかもしれないが,構文定義が大きくなると文脈でなんとかした方が見通しが良くなることもある.もちろんこの機能は,文法クラスの拡張にも使える.基本 PEG はスタック1つ分のマシンで検査できる範囲としたら,文脈にもスタックを持たせることでスタック2つ分の検査ができる.なので文脈の持たせ方によっては,基本チューリング完全な構文検査ができる.
この機能をどうレイアウトルールに適用するかだが,基本的な発想としては,レイアウトルールの前処理関数を文脈操作でエミュレートすると言う感じになる.さて,その前にまず Haskell のレイアウトルールの詳細について説明しておこう.Haskell Language Report に記載されているレイアウトルール [2] の処理は,2段階に分けられる.
- 1段階目はトークンの位置情報を適度に挿入する処理になる.
- 2段階目がその位置情報を見ながらレイアウトトークン「 {」,「 ;」,「 }」を挿入していく.
具体的には次のとおりだ.1段階目は,トークンの列に対して要所要所に以下のレイアウト位置情報を埋め込む:
- {n}
- 新規レイアウト開始. n はレイアウトのインデント位置を表す.
- <n>
- レイアウト中の改行. n は改行時のインデント位置を表す.
処理の内容は以下のようになる:

はトークンの列 を受け取り,適宜レイアウト位置情報を挿入する.例えば,
1 2 3 4 5 6 7 8 9 | module Main where x = case "str" == "str" of True -> Nothing False -> y where y = do z <- Just () pure z f z = z where |
のようなプログラムの場合,
module Main where
{1} x = case "str" == "str" of
{5} True -> Nothing
<5> False -> y where
{9} y = do {16} z <- Just ()
<16> pure z
<1> f z = z where{0}
のようになる.新規レイアウト開始情報は,
- プログラムが module で始まってない場合一番最初
- let, where, do, of の4つのトークンの後
で { が続いていない場合に挿入される.Haskeller の中にはあまり意識していない人も多いかもしれないが,プログラム全体もレイアウトを持っているので,例えば
x = 0 y = 1
のようなプログラムは
{x = 0
}y = 1
のようにレイアウトがちゃんと付かないためパースが失敗する.このような場合に最初に { が挿入されるのは, P が挿入した新規レイアウト開始の情報に依るものだ.module が最初にない場合となっているのは, module ... where の後でもレイアウトを字下げなしで開始できるようにするためのハックだ.詳しくは後述するが,Haskell のレイアウトは今のレイアウトより 1 以上字下げをしないと開始できない.なので,もし「module が最初にない場合」の条件がなければ,
1 2 3 | module Main where x = 0 |
みたいなプログラムは valid にならず,代わりに必ず
1 2 3 | module Main where x = 0 |
のように一文字以上下げてモジュールの本体を書かなければいけなくなる.そこらへんの事情があって,最初だけ特殊な条件が入れてある.
2段目のレイアウト処理では,1段目に挿入されたレイアウト情報とスタックを元に,レイアウトトークンを挿入していく:
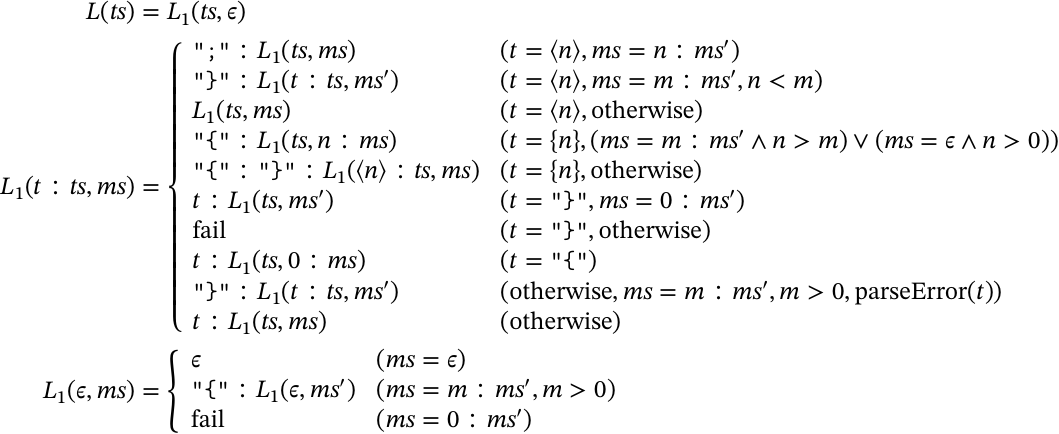
この処理により,最終的に上記で挙げたプログラム
module Main where
{1} x = case "str" == "str" of
{5} True -> Nothing
<5> False -> y where
{9} y = do {16} z <- Just ()
<16> pure z
<1> f z = z where {0}
は,
1 2 3 4 5 6 7 8 9 | module Main where {x = case "str" == "str" of {True -> Nothing ;False -> y where {y = do {z <- Just () ;pure z }}};f z = z where{}} |
のように明示的なレイアウトトークンが挿入された状態に変換される.この処理は大まかには
- レイアウト開始時スタックにレイアウト開始位置をプッシュする.明示的な中括弧の場合は 0 をプッシュする
- 暗黙的な中括弧で開始されたレイアウトについては,スタックとレイアウト位置情報によって適宜レイアウトを閉じ,スタックから対応するレイアウト開始位置をポップする.明示的な中括弧閉じの場合は,スタックの先頭が 0 かチェックしてポップする
と言う感じのことをする.細かく見ていくと,
の規則は,現在レイアウトの位置と一致した改行を見つけると ; を挿入していく.まあこれはいいだろう.
の規則は,現在レイアウトの位置よりインデントが下がった場合は,そこでレイアウトを閉じる.
の規則は,現レイアウトの位置よりインデントが上の場合やレイアウトがまだ開始されていない場合,改行位置情報を無視する.これらにより,改行の情報は現在のレイアウトの状態により適切なレイアウトトークンへと置き換えられる.次に
の規則は,レイアウト開始位置を見て,現在のレイアウトより字下げが行われている場合は中括弧トークンに変換し,スタックにも新しい位置情報を入れておく.その次の規則
では字下げが行われていない場合は即レイアウトを閉じる.また,この場合改行情報だけは残しておく.これらの規則により,
{1} x = 0 where
{5} x1 = 1
<1> y = 0 where
{1} z = 0 where{0}
みたいな場合,
- 最初の {1} を見る場合,スタックが空なため新たなレイアウトを開始し,スタックに 1 をプッシュする
- 次の {5} では,現在のレイアウト位置 1 より字下げしているため,また新たなレイアウトを開始し,スタックに 5 をプッシュする
- 5 のレイアウトは次の <1> で閉じられる
- 次の {1} では,現在のレイアウト位置 1 と同じレイアウト位置なため,レイアウトを即閉じ改行情報を残す.この改行情報により, z の前に ; が挿入される
- 最後の {0} では,現在のレイアウト位置 1 よりレイアウト位置が左にあるため,レイアウトを即閉じ改行情報を残す.この改行情報により,残っているレイアウトも全て閉じられる
という風な処理になり,
1 2 3 4 5 6 | {x = 0 where {x1 = 1 };y = 0 where {};z = 0 where{}} |
というプログラムが出来上がることになる.残りも見ていくと,
は明示的な中括弧閉じの場合,レイアウトが明示的な開始がされたか確認する.明示的な開始でなければ
の規則によりパースを失敗させる.
の規則では,中括弧により明示的なレイアウトを開始する.
の規則は,冒頭で問題にした規則で,パースエラーが起きる位置で暗黙のレイアウトを自動で閉じるというものだ.他の場合は
の規則により単にトークンを受け流していく.最後に入力トークンがなくなった時は,
の規則により,閉じていないレイアウトを閉じていく.その中に明示的な開始によるレイアウトがあった時はパースエラーにする.これが標準仕様の全容になる.
これを文脈付き PEG にどう変換していくかだが,基本的には1段目のレイアウト処理は少し改良しつつそのまま残し,2段目のレイアウト処理を文法に統合するといった感じになる.まず,レイアウト処理を
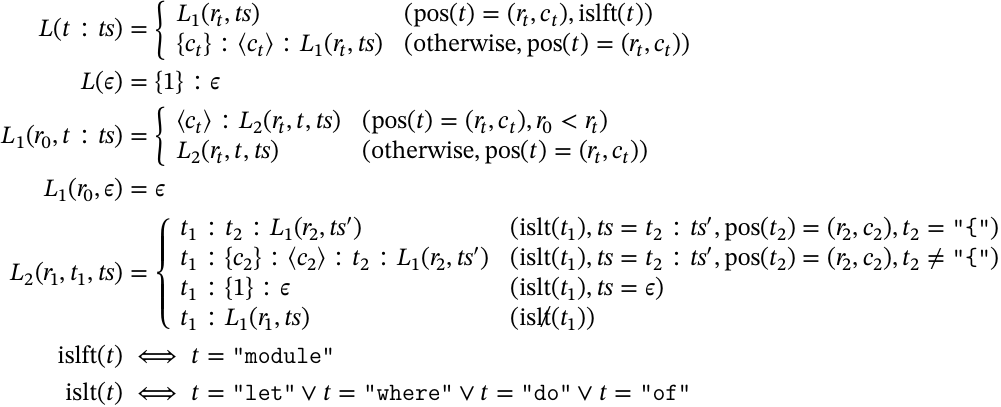
のように変更する.主な変更点は,以下の2点:
- 新規レイアウト開始トークンの後に,改行トークンも続くようにしたこと
- 入力終了時の位置を 0 でなく 1 に変更
その変更の意味は置いといて,文法の方も載せておく:

はレイアウトルールを処理する文法の代表として載せている.レイアウトルールを適用する場所では,このように , , , で囲むようにする.
さて,肝心の文脈操作の方だが,文脈にはレイアウトスタックをそのまま使う. 0 が明示的なレイアウト位置,それより上の値は暗黙的なレイアウトの開始位置を表す., についてはいいだろう. に2つの規則は元々のレイアウト処理関数の
の規則に対応するものになる.最後の一つは,
の規則の一旦を担うものになる.今回の前処理では, {n} の後に <n> が挿入されるため, をスタックにプッシュしておくと強制的にレイアウトの字下げ判定が入り,後段の処理で即 } が挿入されることになる.元の処理と比べて面倒になっているように見えるが,むしろ元の処理は実は {n} がレイアウト開始と改行情報の両方の役割を担っていてそれを今回分離したからだ.実際上で挙げた元のレイアウト処理では, {n} を処理した後後段の処理を <n> を挿入し直して行っている.このトークンの挿入の代わりに,レイアウトを閉じる処理を全て一箇所にまとめるということを今回は行なっている.これが前処理時,元の処理では挿入していなかった <n> をわざわざ {n} の後に挿入するようにした理由になる.
はすごく単純になっている.今回の ptera では Haskell パーサ実装は,PEG で文法を書いているので貪欲にパースが行われる.つまり, にたどり着くということは,それ以上パースできるものがないということに他ならない.つまりはそのままパースを進めるとパースエラーになると言うことだ.これは冒頭に述べたパースエラー時のレイアウト自動終了を体現したものと同時に,字下げ時のレイアウト自動終了も包含している.今回の文法では,レイアウトの改行情報を扱うのは の規則と の規則だけだ.そしてこれらの規則では,現在のレイアウトの開始位置以降に改行位置がある場合のみパースが成功する.逆に言えばレイアウト開始位置より手前の場合,パースに失敗する.これにより,字下げ時 がリデュースされる感じになる.
はまあいいだろう. は特殊な非終端記号.この規則は全ての終端記号の手前で評価される.例えば,
A ::= "b" A "c"
みたいな規則があった時,これは
A ::= skip "b" A skip "c"
みたいな感じになる.これにより各トークンが消費される際,レイアウトに関与しない改行情報はスキップすることで,レイアウト処理を完結させていく.この特殊な非終端記号については,ptera では特に特別な機能を入れず対応しており,終端記号を作る API をラップし必ず がその手前に来るようにしている.
完全なパーサの規則については,https://github.com/mizunashi-mana/ptera/blob/ptera-th-0.2.0.0/example/haskell2010/src/Parser/Rules.hs を参照して欲しい.この規則により,GHC よりかなり見通しの良いパーサが実装でき,また例を見てもらうと分かると思うが,PEG で文法を書くことでほぼ Haskell Language Report の規則をそのまま表現できるという感じ [6].
文脈を考慮した SRB
さて,ここまでは文脈付き PEG で何を実現したいかの話をしてきたが,では具体的に文脈付き PEG パーサをどう生成するかの話もしておく. 前回 は,最終的に PEG を SRB という機械に変換し,パーサを生成する方法を紹介した.今回もその方法は基本的に変更はない.ただし,SRB を文脈を考慮して修正したのと,先読みの強化をおこなっている.まずは,SRB の修正部分について話しておこう.といっても,修正自体は文脈が変わったらメモリをまっさらにするだけだが.
まず,文脈操作アクションを文法規則に付与する.具体的には,規則それぞれに対しコンテキストを受け取って以下を返す関数を付与する:
- 更新なし
- コンテキストを に更新する
- リデュースを失敗させる
コンテキストの集合を としてこれらの集合を と表現する時,アクションは のような関数となる.この関数は,例えば
{ l ↦ l | front(l) = "a" }
のような文脈操作は,
のような関数で表現する.この関数を SRB の操作,, にパラメータとして付与する.そして,これを元に SRB の意味論を以下のように修正する:

異なる部分は,
- 文脈をそれぞれの状態に付与する
- 文脈が変わったタイミングでメモは抹消
- 過去の文脈は覚えておき,バックトラック時に必要に応じて文脈を戻す
という感じ.なお,過去の文脈を全て覚えておくのはいささか微妙だが,実際の実装ではバックトラックが発生する場合のみ必要な文脈だけを覚えておくようにしている.こんな感じで,少々手を加えれば SRB の方は対応できる.
先読みの強化
さて,今回の実装でもう一つ大きく変更したのが,先読みの強化だ.ptera の実装は先読みによりバックトラックをなるべく少なくすることで,実用的なパースを行おうというものだ.ただ,今までの実装は 規則をどこかに含んでいるとそこで先読みを諦めてしまう.例えば,
abc :: ab "c" ab ::= "a" | "b" |
みたいな規則があった時,通常 の1文字先読み結果は a / b / c になるが,これまでの ptera は の先読みに の結果をそのまま使っていた.そして, の先読みは何が次に来ても良いと言うものだったので, の結果も全てを許容するというものになり, もそれを継承することになる.その結果先読みが機能せず,無駄なバックトラックが発生しやすくなってしまう.特に今回の Haskell パーサの実装では,終端記号の前に 規則を含む 記号が置かれるため,ほとんど先読みが機能しなくなってしまっていた.そこで,もう少し先読みを強化してみるかと言う感じになった.
今までの先読みは先に続く文字で許容するものを特定すると言うものだったが,先読み強化にあたって何もトークンを消費しないで先に行ける空遷移 (イプシロン遷移)とトークンを消費する場合の先読み情報を明確に区別するようにした.これにより,上の例で今まで の先読み情報は「次に何があっても良い」と言うものだったのが,「a / b を消費して進むかまたは空遷移」というものに変わる.これにより, の先読みの際 の先読み情報見つつ,空遷移の場合はさらに先を見てみて c を必ず消費するので,先読み結果は「a / b / c いずれかを消費し進む」と結論づけることができるみたいな感じ.
ただ,この修正で変更すべき範囲は結構広い.今までは規則のそれぞれの位置で非終端記号があるならその非終端記号の先読み情報をそのまま使う,終端記号であればそれをそのまま先読み情報とするみたいな感じで先読みを行なっていた.ところが,今回の変更を適用するためには非終端記号の場合先読み情報をそのまま使えるわけではなく,空遷移が入っている場合はさらに先を読む必要が出てくる.そこら辺を踏まえ大きくアルゴリズムを修正することになった.修正した先読みのアルゴリズムは以下のようになる:

このアルゴリズムは最終的に,PEG の各規則ごとにその先読み結果をつけた先読みテーブルを返す.先読みはそれぞれ,消費が発生する場合の消費する可能性のあるトークンの集合と,空遷移が発生するかの真偽値の組から成っている.今回の先読みアルゴリズムは二段構成になっており,まず非終端記号それぞれに対する先読みを行なった後,その結果を元に各規則の正確な先読みを行うようになっている.これはそうしないで正確な先読み一回で済まそうとすると,先読みが循環して正確に行えない場合があるからだ.先読み自体は,空遷移があるなら後ろの先読み結果も使う,空遷移がないなら先読みはそこで完結みたいな感じのことを書き下すとこうなると言う感じ.後は否定の場合を少しだけ正確にしている(といっても焼け石に水という感じだが).とりあえず,これにより否定が入らないなら本当の1文字先読みが実現できるはず.
まとめ
Haskell パーサが割とちゃんと狙い通りに実現できたので満足している.また先読み強化により,Haskell パーサのバックトラックも劇的に改善した.もう少し考えるべき点はまあまだもう少しあるんだが,とりあえず今回はこれで満足.後はまた使いながら改善していこうかなと.
当初は PEG 使えば割と楽できるんじゃね?と雑に考えていたが,PEG は PEG なりに苦労する部分があると気づけたのは大きいと思う.また,PEG そのものではないが,PEG に文脈をつけてもそれなりに何とかなり,レイアウトルールを割と綺麗に扱えるっぽいと分かったのも良かった.とりあえず,これで ptera 弄るのは一段楽かなという感じ.今回はこれで.
| [1] | モジュール修飾子周りの仕様は,実装者に優しいかと言われるとちょっと微妙な気もするが. |
| [2] | (1, 2) https://www.haskell.org/onlinereport/haskell2010/haskellch10.html#x17-17800010.3 |
| [3] | Haskell 98 から Haskell 2010 でレイアウトルールの仕様が一部変わったりなどや,構文を拡張する GHC 拡張などの影響も大きいが.最近でまだ閉じれられていないレイアウトルール関連の問題としては,https://gitlab.haskell.org/ghc/ghc/-/issues/17359 があるようだ. |
| [4] | https://github.com/haskell-suite/haskell-src-exts/issues/282 |
| [5] | HSE もそれに倣ってか,同じようにトークナイザとパーサが連動している.PureScript などの Haskell 系列のものも大体似たようなことをやっているあたり,かなり根深い問題であると言うことだろう. |
| [6] | 最も左再帰や曖昧性がある箇所については修正が必要で,その部分は少しずれているが. |