colimit としての自然数の集合

Posted on 金 30 8月 2019 in 数学

F;i↦{n∣n≤i}:N→PosetF; i \mapsto \{n \mid n \leq i\}: \mathbb{N} \to \mathrm{Poset} みたいな directed diagram を考えた時，こいつの colimit は何になるか考えようという話が降ってきたんだけど，圏論弱者で頭が混乱してしまって解けなかったので，色々考えたメモ．

directed colimit

ある圏 CC と圏 II からの図式 F:I→CF: I \to C を考える．この時， FF の colimit とは， CC の対象 colimF∈∣C∣\mathop{\mathrm{colim}} F \in |C| と cocone μ:F⇒Δ(colimF)\mu: F \Rightarrow \Delta (\mathop{\mathrm{colim}} F) の組で，以下の普遍性を満たすもの:

∀φ:F⇒ΔX.∃!f:colimF→X.μ;Δ(f)=φ \forall \varphi: F \Rightarrow \Delta X\ldotp \exists ! f: \mathop{\mathrm{colim}} F \to X\ldotp \mu; \Delta(f) = \varphi

ただし， Δ:C→CI\Delta: C \to C^I は対角関手．

diagram の index が directed set である場合に，それ上の colimit を directed colimit と呼ぶ．とりあえずここまでが導入．

colimit としての N\mathbb{N}

F;i→{n∣n≤i}:N→PosetF; i \to \{n \mid n \leq i\}: \mathbb{N} \to \mathrm{Poset} のような diagram を考える．射は単純に F(i≤j);n↦nF(i \leq j); n \mapsto n で作れる．こいつの directed colimit は何になるだろう？ 直感的には，最終的に N\mathbb{N} に収束しそうだ．確かめてみる．

まず colimit cocone は μi;x↦x:{n∣n≤i}→N\mu_i; x \mapsto x: \{n \mid n \leq i\} \to \mathbb{N} で考えられそうだ．さて， φ:F⇒ΔX\varphi: F \Rightarrow \Delta X に対して， μ;Δ(f)=φ\mu; \Delta(f) = \varphi を満たす f:N→Xf: \mathbb{N} \to X を考えてみる．

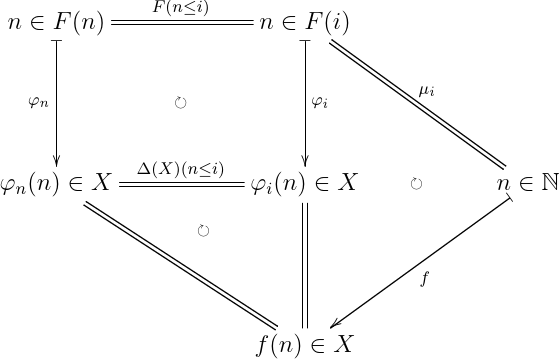
一意性について，計算している図式．

つまり任意の ff について， f(n)=φn(n)f(n) = \varphi_n(n) が成り立ち，逆に n↦φn(n)n \mapsto \varphi_n(n) を考えればこれは一意で等式を満たす射ということになる．ここから， N\mathbb{N} は FF の colimit となる．

Cpo での colimit

さて実は本題はここからで， {n∣n≤i}\{n \mid n \leq i\} は finite poset でありつまり cpo だ．なので先ほどの FF は N\mathbb{N} から Cpo\mathrm{Cpo} への図式としても考えられる．この場合， FF の colimit は何になるだろう？ 問題は， N\mathbb{N} は cpo でないことだ． N\mathbb{N} 全体を考えると，こいつは directed set になるが sup を持たないからだ．では， FF の colimit は無いのだろうか？

実は， N\mathbb{N} は cpo では無いのだが N∞=N∪{∞}\mathbb{N}_{\infty} = \mathbb{N} \cup \{\infty\} は cpo になる．こいつに対して Poset\mathrm{Poset} での構成を試してみる． N\mathbb{N} の範囲では同じ話を適用できる．が， f(∞)f(\infty) が一意に決まるかは分からないので， colimit を考えられないように見える．しかし，実はこいつを決められる要素が， Cpo\mathrm{Cpo} にはある．それが連続性だ．今回の場合 f:N∞→Xf: \mathbb{N}_{\infty} \to X は連続関数なので，次の式が成り立つ:

f(∞)=f(⨆n∈Nn)=⨆n∈Nf(n)=⨆n∈Nφn(n) f(\infty) = f(\bigsqcup_{n \in \mathbb{N}} n) = \bigsqcup_{n \in \mathbb{N}} f(n) = \bigsqcup_{n \in \mathbb{N}} \varphi_n(n)

XX が cpo なので，こいつは well-defined で sup は一意より， ff は N∞\mathbb{N}_{\infty} 全域で一意に定めることができる．ここから， F:N→CpoF: \mathbb{N} \to \mathrm{Cpo} の colimit は N∞\mathbb{N}_{\infty} になる．

Poset\mathrm{Poset} と Cpo\mathrm{Cpo}

ここまで見て，混乱した人はいないだろうか？ 僕は当初混乱した． N∞\mathbb{N}_{\infty} が Cpo\mathrm{Cpo} で colimit になれるなら，なぜ Poset\mathrm{Poset} では慣れなかったのだろう？ もしかして， N\mathbb{N} と N∞\mathbb{N}_{\infty} って poset として同型なのか？ とか本気で考えた (そんなバカな話はもちろん成り立たない) ．なので，最後に Poset\mathrm{Poset} と Cpo\mathrm{Cpo} で何が違うのか見てみる．

Poset\mathrm{Poset} の中で N∞\mathbb{N}_{\infty} から N\mathbb{N} への一意射が作れないか考えてみる．先ほどの話から，問題は f(∞)f(\infty) の定め方にあることは分かるだろう．こいつをどう定めるかが問題になるわけだけど， Poset\mathrm{Poset} の射は単調である必要があるので，

∀n∈N.f(∞)≥f(n)=n \forall n \in \mathbb{N}\ldotp f(\infty) \geq f(n) = n

を満たす必要がある．ここまでくるとみなさんお気づきだと思うけど， N\mathbb{N} は上限を持たないので，これを満たすように ff をうまく作れないのだ．これが， Poset\mathrm{Poset} と Cpo\mathrm{Cpo} の大きな違いっぽくて， Cpo\mathrm{Cpo} は directed subset でさえ sup を持てないようなものを除外することで well-defined 性をうまく保証してくれるっぽい．なので，連続性を用いて一意にうまく定めることができるけど， Poset\mathrm{Poset} ではそこがうまくいかない，一意射の一意性どころか構成できないというわけだ．

まとめ

これは完全に知らない話だったので，ほへーってなった．また一つ賢くなってしまった (順序理論界隈とかだと常識かもしれないので，無知を晒してしまったとも言う)． Cpo\mathrm{Cpo} は Poset\mathrm{Poset} の full subcategory だと無邪気に信じてたが，こうなると怪しそう．埋め込みうまく作る方法あったりするんだろうか？ 時間ができたらちょっと考えてみたい．

Domain Theory 束論 順序理論

You might enjoy